Linear Regression 📈
MSSC 6250 Statistical Machine Learning
Department of Mathematical and Statistical Sciences
Marquette University
Linear Regression (Review)
Linear Regression
Linear regression is an approach to supervised learning.
It assumes that the dependence of \(Y\) on \(X_1, X_2, \dots, X_k\)1 is linear.
True regression functions \(f(x)\) are never linear!
Although it is overly simplistic, the linear model has distinct advantages in terms of its interpretability and often shows good predictive performance.
Why Multiple Linear Regression (MLR) Model
- Our target response may be affected by several factors.
- Total
sales\((Y)\) and amount of money spent on advertising onYouTube(YT) \((X_1)\),Facebook(FB) \((X_2)\),Instagram(IG) \((X_3)\).1


- Predict sales based on the three advertising expenditures and see which medium is more effective.
Fit Separate Simple Linear Regression (SLR) Models
❌ Fitting a separate SLR model for each predictor is not satisfactory.
Don’t Fit a Separate Simple Linear Regression
- 👉 How to make a single prediction of sales given levels of the 3 advertising media budgets?
- How to predict the sales when the amount spent on YT is 50, 100 on FB and 30 on IG?
- 👉 Each regression equation ignores the other 2 media in forming coefficient estimates.
- The effect of FB advertising on sales may be increased or decreased when YT and IG advertising are in the model.
- IG advertising may have no impact on sales when YT and FB advertising are in the model.
- 👍👍 Better approach: extend the SLR model so that it can directly accommodate multiple predictors.
Multiple Linear Regression Model
- The population MLR model: \[Y_i= \beta_0 + \beta_1X_{i1} + \beta_2X_{i2} + \dots + \beta_kX_{ik} + \epsilon_i\]
- In the advertising example, \(k = 3\) and \[\texttt{sales} = \beta_0 + \beta_1 \times \texttt{YouTube} + \beta_2 \times \texttt{Facebook} + \beta_3 \times \texttt{Instagram} + \epsilon\]
- Model assumptions:
- \(\epsilon_i \stackrel{iid}{\sim} N(0, \sigma^2)\)
How many parameters are there in the model?
Sample MLR Model
- Given the training sample \((x_{11}, \dots, x_{1k}, y_1), (x_{21}, \dots, x_{2k}, y_2), \dots, (x_{n1}, \dots, x_{nk}, y_n),\)
- The sample MLR model to be trained: \[\begin{align*} y_i &= \beta_0 + \beta_1x_{i1} + \beta_2x_{i2} + \dots + \beta_k x_{ik} + \epsilon_i \\ &= \beta_0 + \sum_{j=1}^k\beta_j x_{ij} + \epsilon_i, \quad i = 1, 2, \dots, n \end{align*}\]
Regression Hyperplane
- SLR: regression line
- MLR: regression hyperplane or response surface
- \(y = \beta_0 + \beta_1x_1 + \beta_{2}x_2 + \epsilon\)
- \(E(y \mid x_1, x_2) = 50 + 10x_1 + 7x_2\)
Response Surface
- \(y = \beta_0 + \beta_1x_1 + \beta_{2}x_2 + \beta_{11}x_1^2 + \beta_{22}x_2^2 + \beta_{12}x_1x_2 + \epsilon\)
- \(E(y \mid x_1, x_2) = 800+10x_1+7x_2 -8.5x_1^2-5x_2^2- 4x_1x_2\)
- 😎 🤓 A linear regression model can describe a complex nonlinear relationship between the response and predictors!
Ordinary Least Squares Estimation of the Coefficients
\[\begin{align*} y_i &= \beta_0 + \beta_1x_{i1} + \beta_2x_{i2} + \dots + \beta_k x_{ik} + \epsilon_i \\ &= \beta_0 + \sum_{j=1}^k\beta_j x_{ij} + \epsilon_i, \quad i = 1, 2, \dots, n \end{align*}\]
- The least-squares function Sum of Squared Residuals (\(SS_{res}\))1 is \[SS_{res}(\alpha_0, \alpha_1, \dots, \alpha_k) = \sum_{i=1}^n\left(y_i - \alpha_0 - \sum_{j=1}^k\alpha_j x_{ij}\right)^2\]
- \(SS_{res}\) must be minimized with respect to the coefficients, i.e., \[(b_0, b_1, \dots, b_k) = \underset{{\alpha_0, \alpha_1, \dots, \alpha_k}}{\mathrm{arg \, min}} SS_{res}(\alpha_0, \alpha_1, \dots, \alpha_k)\]
Geometry of Least Squares Estimation
Least-squares Normal Equations
\[\begin{align*} \left.\frac{\partial SS_{res}}{\partial\alpha_0}\right\vert_{b_0, b_1, \dots, b_k} &= -2 \sum_{i=1}^n\left(y_i - \alpha_0 - \sum_{j=1}^k \alpha_j x_{ij}\right) = 0\\ \left.\frac{\partial SS_{res}}{\partial\alpha_j}\right\vert_{b_0, b_1, \dots, b_k} &= -2 \sum_{i=1}^n\left(y_i - \alpha_0 - \sum_{j=1}^k \alpha_j x_{ij}\right)x_{ij} = 0, \quad j = 1, 2, \dots, k \end{align*}\]
\(k + 1\) equations with \(k + 1\) unknown parameters.
The ordinary least squares estimators are the solutions to the normal equations.
🍹 🍺 🍸 🥂 I buy you a drink if you solve the equations by hand without using matrix notations or operations!
Interpreting Coefficients
Estimate Std. Error t value Pr(>|t|)
(Intercept) 2.939 0.312 9.422 0.00
youtube 0.046 0.001 32.809 0.00
facebook 0.189 0.009 21.893 0.00
instagram -0.001 0.006 -0.177 0.86\[\hat{y} = b_0 + b_1 x_1 + \cdots + b_kx_k\]
\[\widehat{\texttt{sales}} = 2.939 + 0.046 \times \texttt{YouTube} + 0.189 \times \texttt{Facebook} - 0.001 \times \texttt{Instagram}\]
-
\(b_1\): Holding all other predictors fixed, for one unit increase of
Youtube, thesalesis expected to be increased, on average, by 0.046 units. -
\(b_2\): All else held constant, one unit increase of
Facebookleads to, on average, 0.189 unit increase ofsales. -
\(b_0\): The
saleswith no expenditures onYoutube,Facebook, andInstagramis expected to be 2.939. (Make sense?!)
Inference on Coefficients
- The \((1-\alpha)100\%\) Wald confidence interval (CI) for \(\beta_j\), \(j = 0, 1, \dots, k\) is
\[\left(b_j- t_{\alpha/2, n-p}~se(b_j), \quad b_j + t_{\alpha/2, n-p}~ se(b_j)\right)\]
2.5 % 97.5 %
(Intercept) 2.32 3.55
youtube 0.04 0.05
facebook 0.17 0.21
instagram -0.01 0.01Important
These are marginal CIs seperately for each \(b_j\).
Individual CI ignores the correlation between \(b_j\)s.
Better to consider elliptically-shaped regions.
Collinearity
Interpretation makes sense when predictors are not highly correlated.
-
Correlations amongst predictors cause problems (Collinearity).
- Large variance of coefficients.
- Large magnitude of coefficients.
- Instable and wrong signed coefficients.
Note
Think about the standard error size. Do we tend to conclude \(\beta_j = 0\) or not?
Extrapolation
- Regression models are intended as interpolation equations over the range of the regressors used to fit the model.
Note
Do not use regression for time series forecasting!
Regression is Not for Causal Inference

Practical Significance vs. Statisical Significance
Important
-
\(H_0:\beta_j = 0\) will always be rejected as long as the sample size is large enough, even \(x_j\) has a very small effect on \(y\).
- Consider the practical significance of the result, not just the statistical significance.
- Use confidence intervals to draw conclusions instead of relying only on p-values.
Important
- If the sample size is small, there may not be enough evidence to reject \(H_0:\beta_j = 0\).
- Do Not immediately conclude that the variable has no association with the response.
- There may be a linear association that is just not strong enough to detect given your data, or there may be a non-linear association.
Test for significance
Test for significance: Determine if there is a linear relationship between the response and any of the regressor variables.
\(H_0: \beta_1 = \beta_2 = \cdots = \beta_k = 0 \quad H_1: \beta_j \ne 0 \text{ for at least one } j\)

\(\sum_{i=1}^n(y_i - \overline{y})^2 = \sum_{i=1}^n(\hat{y}_i - \overline{y})^2 + \sum_{i=1}^n(y_i - \hat{y}_i)^2\)
Reject \(H_0\) if \(F_{test} > F_{\alpha, k, n - k - 1}\).
What is the sample statistic we use to accesses how well the model fits the data?
Reduced Model vs. Full Model
- Overall test of significance: all predictors vs. Marginal \(t\)-test: one single predictor
- How to test any subset of predictors?
- Full Model: \(y = \beta_0 + \beta_1x_1+\beta_2x_2 + \beta_3x_3 + \beta_4x_4 + \epsilon\)
- \(H_0: \beta_{2} = \beta_{4} = 0\)
- Reduced Model (under \(H_0\)): \(y = \beta_0 + \beta_1x_1 + \beta_3x_3 + \epsilon\)
- Like to see if \(x_2\) and \(x_4\) can contribute significantly to the regression model when \(x_1\) and \(x_3\) are in the model.
- If yes, \(\beta_{2} \ne 0\) and/or \(\beta_{4} \ne 0\). (Reject \(H_0\))
- Otherwise, \(\beta_{2} = \beta_{4} = 0\). (Do not reject \(H_0\))
Given \(x_1\) and \(x_3\) in the model, we examine how much extra \(SS_R\) is increased (\(SS_{res}\) is reduced) if \(x_2\) and \(x_4\) are added to the model.
Extra-sum-of-squares and Partial \(F\)-test
\(F_{test} = \frac{SS_R(\beta_2, \beta_4 \mid \beta_1, \beta_3)/r}{SS_{res}/(n-k-1)} = \frac{MS_R(\beta_2, \beta_4 \mid \beta_1, \beta_3)}{MS_{res}}\) where \(r\) is the number of coefficients being tested.
Under \(H_0\) that \(\beta_{2} = \beta_{4} = 0\), \(F_{test} \sim F_{r, n-k-1}\).
Reject \(H_0\) if \(F_{test} > F_{\alpha, r, n-k-1}\).
Given the regressors of \(x_1, x_3\) are in the model,
If the regressors of \(x_2\) and \(x_4\) contribute much, \(SS_R(\beta_2, \beta_4 \mid \beta_1, \beta_3)\) will be large.
A large \(SS_R(\beta_2, \beta_4 \mid \beta_1, \beta_3)\) implies a large \(F_{test}\).
A large \(F_{test}\) tends to reject \(H_0\), and conclude that \(\beta_{2} \ne 0\) and/or \(\beta_{4} \ne 0\).
The regressors of \((x_2, x_4)\) provide additional explanatory and prediction power that \((x_1, x_3)\) cannot provide.
Regression Model in Matrix Form
\[y_i= \beta_0 + \beta_1x_{i1} + \beta_2x_{i2} + \dots + \beta_kx_{ik} + \epsilon_i, \quad \epsilon_i \stackrel{iid}{\sim} N(0, \sigma^2), \quad i = 1, 2, \dots, n\]
\[\bf y = \bf X \boldsymbol{\beta} + \boldsymbol{\epsilon}\] where
\[\begin{align} \bf y = \begin{bmatrix} y_1 \\ y_2 \\ \vdots \\ y_n \end{bmatrix},\quad \bf X = \begin{bmatrix} 1 & x_{11} & x_{12} & \cdots & x_{1k} \\ 1 & x_{21} & x_{22} & \cdots & x_{2k} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 1 & x_{n1} & x_{n2} & \cdots & x_{nk} \end{bmatrix}, \quad \boldsymbol{\beta} = \begin{bmatrix} \beta_0 \\ \beta_1 \\ \vdots \\ \beta_k \end{bmatrix} , \quad \boldsymbol{\epsilon} = \begin{bmatrix} \epsilon_1 \\ \epsilon_2 \\ \vdots \\ \epsilon_n\end{bmatrix} \end{align}\]
- \({\bf X}_{n \times p}\): Design matrix
- \(\boldsymbol{\epsilon} \sim MVN_n({\bf 0}, \sigma^2 {\bf I}_n)\)1
Least Squares Estimation in Matrix Form
\[\begin{align} S(\boldsymbol{\beta}) = \sum_{i=1}^n\epsilon_i^2 = \boldsymbol{\epsilon}'\boldsymbol{\epsilon} &= (\bf y - \bf X \boldsymbol{\beta})'(\bf y - \bf X \boldsymbol{\beta}) \\ &= \bf y'\bf y - \boldsymbol{\beta}'\bf X'\bf y - \bf y'\bf X \boldsymbol{\beta} + \boldsymbol{\beta}' \bf X' \bf X \boldsymbol{\beta} \\ &={\bf y}'{\bf y} - 2\boldsymbol{\beta}'{\bf X}'{\bf y} + \boldsymbol{\beta}' {\bf X}' {\bf X} \boldsymbol{\beta} \end{align}\]
Let \({\bf t}\) and \({\bf a}\) be \(n \times 1\) column vectors, and \({\bf A}_{n \times n}\) is a symmetric matrix.
\(\frac{\partial {\bf t}'{\bf a} }{\partial {\bf t}} = \frac{\partial {\bf a}'{\bf t} }{\partial {\bf t}} = {\bf a}\)
\(\frac{\partial {\bf t}'{\bf A} {\bf t}}{\partial {\bf t}} = 2{\bf A} {\bf t}\)
- Normal equations: \(\begin{align} \left.\frac{\partial S}{\partial \boldsymbol{\beta}}\right \vert_{\bf b} = -2 {\bf X}' {\bf y} + 2 {\bf X}' {\bf X} {\bf b} = \boldsymbol{0} \end{align}\)
- LSE for \(\boldsymbol{\beta}\): \(\begin{align} \boxed{{\bf b} = \arg \min _{\boldsymbol{\beta}} (\bf y - \bf X \boldsymbol{\beta})'(\bf y - \bf X \boldsymbol{\beta}) = ({\bf X}' {\bf X}) ^{-1} {\bf X}' \bf y} \end{align}\) provided that \({\bf X}' {\bf X}\) is full rank.
Normal Equations
\((\bf X' \bf X) \bf b = \bf X' \bf y\)
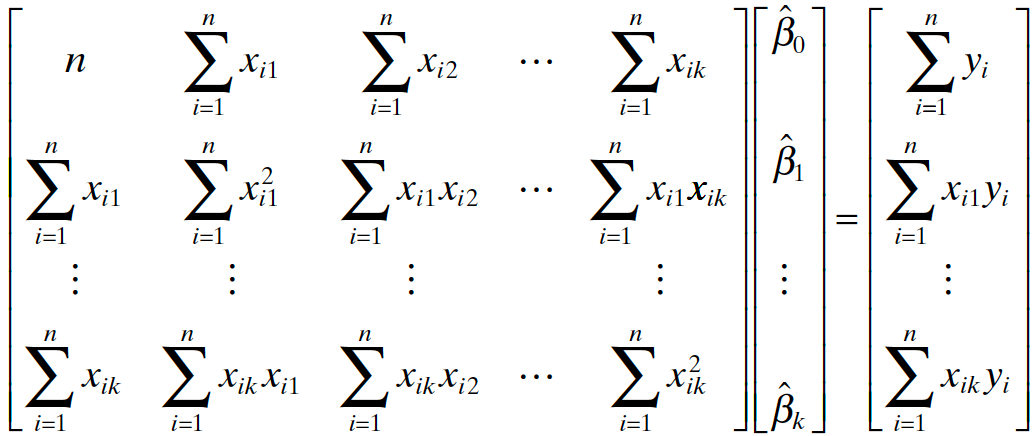
Hat Matrix
\[\hat{\bf y} = {\bf X} {\bf b} = {\bf X} ({\bf X}' {\bf X}) ^{-1} \bf X' \bf y = \bf H \bf y\]
The hat matrix \({\bf H}_{n \times n} = {\bf X} ({\bf X}' {\bf X}) ^{-1} \bf X'\)
The vector of residuals \(e_i = y_i - \hat{y}_i\) is \[\bf e = \bf y - \hat{\bf y} = \bf y - \bf X \bf b = \bf y -\bf H \bf y = (\bf I - \bf H) \bf y\]
Both \(\bf H\) and \(\bf I-H\) are symmetric and idempotent. They are projection matrices.
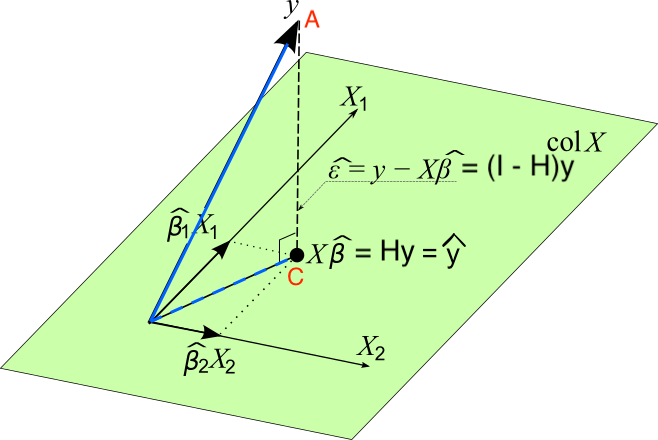
\(\bf H\) projects \(\bf y\) to \(\hat{\bf y}\) on the \((k+1)\)-dimensional space spanned by columns of \(\bf X\), or the column space of \(\bf X\), \(Col(\bf X)\).
\(\bf I - H\) projects \(\bf y\) to \(\bf e\) on the space perpendicular to \(Col(\bf X)\), or \(Col(\bf X)^{\bot}\).
Geometrical Interpretation of Least Squares
\(Col({\bf X}) = \{ {\bf Xb}: {\bf b} \in {\bf R}^{k+1} \}\), \({\bf y} \notin Col({\bf X})\)
\(\hat{{\bf y}} = {\bf Xb} = {\bf H} {\bf y} \in Col({\bf X})\)
\(\small {\bf e} = ({\bf y - \hat{\bf y}}) = ({\bf y - X b}) = ({\bf I} - {\bf H}) {\bf y} \perp Col({\bf X})\)
\({\bf X}'{\bf e} = 0\)
Searching for \(\bf b\) that minimizes \(SS_{res}\) is equivalent to locating the point \({\bf Xb} \in Col({\bf X})\) \((C)\) that is as close to \(\bf y\) \((A)\) as possible!
Multivariate Gaussian/Normal Distribution
-
\({\bf y} \sim N_n(\boldsymbol \mu, {\bf \Sigma})\)
- \(\boldsymbol \mu\): \(n \times 1\) mean vector
- \({\bf \Sigma}\): \(n \times n\) covariance matrix
- \(\boldsymbol \mu= (2, 1)'\); \({\bf \Sigma} = \begin{pmatrix} 2 & -1 \\ -1 & 2\end{pmatrix}\)
Sampling Distribution of \({\bf b}\)
\({\bf y} \sim N(\boldsymbol \mu, {\bf \Sigma})\), and \({\bf Z = By + c}\) with a constant matrix \({\bf B}\) and vector \(\bf c\), then \[{\bf Z} \sim N({\bf B\boldsymbol \mu}, {\bf B \Sigma B}')\]
\({\bf b} = ({\bf X}' {\bf X}) ^{-1} \bf X' \bf y\)
\[\textbf{b} \sim N\left(\boldsymbol \beta, \sigma^2 {\bf (X'X)}^{-1} \right)\] \[E(\textbf{b}) = E\left[ {\bf (X'X)}^{-1} {\bf X}' {\bf y}\right] = \boldsymbol \beta\] \[\mathrm{Var}(\textbf{b}) = \mathrm{Var}\left[{\bf (X'X)}^{-1} {\bf X}' {\bf y} \right] = \sigma^2 {\bf (X'X)}^{-1}\]
The unknown \(\sigma^2\) is estimated by \(\hat{\sigma}^2 = MS_{res} = \frac{SS_{res}}{n - k - 1}\).
\(\textbf{b}\) is Best Linear Unbiased Estimator (BLUE) (Gauss-Markov Theorem).
What is Not Covered
Detailed statistical inference
Regression Diagnostics (Usual Data: Outliers, leverage points, influential points; Non-normality; Non-constant variance; Non-linearity)
Categorical variables
Model/Variable Selection
Code for doing regression (
lm()in R andlinear_model.LinearRegression()insklearnof Python)Maximum likelihood estimation
Where to learn these stuff?
Dr. Yu’s MSSC 5780 slides https://math4780-f23.github.io/website/
ISL Ch 3, 6.1.
Generalizations of the Linear Model
Classification: logistic regression, support vector machines
Non-linearity: kernel smoothing, splines and generalized additive models, nearest neighbor methods.
Interactions: Tree-based methods, bagging, random forests and boosting
Shrinkage and Regularization: Ridge regression and LASSO
Numerical Optimization for Linear Regression
Basic Concepts
- Although we have the closed form for \({\bf b} = ({\bf X}' {\bf X}) ^ {-1} {\bf X}' {\bf y}\), we can solve for \(\bf b\) numerically.
\[\begin{align} \underset{\boldsymbol \beta}{\text{min}} \quad \ell(\boldsymbol \beta) = \frac{1}{n} \sum_i (y_i - \beta_0 - x_i\beta_1)^2 \\ \end{align}\]
- \(\ell(\boldsymbol \beta)\), the \(\text{MSE}_{\texttt{Tr}}\), is called the (squared) loss function.
- Start with an initial value of \(\boldsymbol \beta\), say \(\widehat{\boldsymbol \beta} = (0.3, 1.5)\), we compute the \(\text{MSE}_{\texttt{Tr}}\)
\[\begin{align} \frac{1}{n}\sum_i \left( y_i - 0.3 - 1.5 x_i \right)^2 \\ \end{align}\]
Basic Concepts
# calculate the residual sum of squares for a grid of beta values
mse <- function(b, trainx, trainy) mean((trainy - b[1] - trainx * b[2]) ^ 2)
mse(b = c(0.3, 1.5), trainx = x, trainy = y)[1] 1.250039- The initial point \((0.3, 1.5)\) is not at the bottom of the surface.
optim()1
Basic Principles
For a general function \(f(\mathbf{x})\) to be minimized with respect to (w.r.t.) \(\mathbf{x}\in \mathbf{R}^{p}\), we have
- First-Order Necessary Condition:
If \(f\) is continuously differentiable in an open neighborhood of local minimum \(\mathbf{x}^\ast\), then \(\nabla f(\mathbf{x}^\ast) = \mathbf{0}\).
Taylor Expansion
\[f(\mathbf{x}^\text{new}) \approx f(\mathbf{x}) + \nabla f(\mathbf{x}) (\mathbf{x}^\text{new} - \mathbf{x})\]
- Whether \(\nabla f(\mathbf{x})\) is positive or negative, we can always find a new point \(\mathbf{x}^\text{new}\) that makes \(\nabla f(\mathbf{x}) (\mathbf{x}^\text{new} - \mathbf{x})\) less than 0, so that \(f(\mathbf{x}^\text{new}) < f(\mathbf{x})\).
\(\nabla f(\mathbf{x}^\ast) = \mathbf{0}\) is only a necessary condition, not a sufficient condition.
\(x = 1\) is a local minimizer, not a global one.
Second-order Property
Second-order Sufficient Condition:
\(f\) is twice continuously differentiable in an open neighborhood of \(\mathbf{x}^\ast\). If \(\nabla f(\mathbf{x}^\ast) = \mathbf{0}\) and \(\nabla^2 f(\mathbf{x}^\ast)\) , the Hessian matrix, is positive definite, i.e., \[ \nabla^2 f(\mathbf{x}) = \left(\frac{\partial^2 f(\mathbf{x})}{\partial x_i \partial x_j}\right) = \mathbf{H}(\mathbf{x}) \succeq 0 \] then \(\mathbf{x}^\ast\) is a strict local minimizer of \(f\).
\[\begin{align} \text{Left:} \qquad \nabla^2 f_1(x) &= 2 \\ \text{Right:} \qquad \nabla^2 f_2(x) &= 12x^2 + 12 x - 10\\ \end{align}\]
- For \(f_1\), \(\mathbf{H}(\mathbf{x}) \succeq 0\), and the solution is a minimizer.
- For \(f_2\), \(\nabla^2 f_2(-2.5) = 35\), \(\nabla^2 f_2(0) = -10\) and \(\nabla^2 f_2(1) = 14\). So \(x = -2.5\) and \(1\) are local minimizers and \(0\) is a local maximizer.
Optimization Algorithm
1. Start with \(\mathbf{x}^{(0)}\)
- For \(i = 1, 2, \dots\) until convergence, find \(\mathbf{x}^{(i)}\) s.t. \(f(\mathbf{x}^{(i)}) < f(\mathbf{x}^{(i-1)})\)
- Stopping criterion:
- Gradient of the objective function: \(\lVert \nabla f(\mathbf{x}^{(i)}) \rVert < \epsilon\)
- (Relative) change of distance: \(\frac{\lVert \mathbf{x}^{(i)} - \mathbf{x}^{(i-1)} \rVert} {\lVert \mathbf{x}^{(i-1)}\rVert}< \epsilon\) or \(\lVert \mathbf{x}^{(i)} - \mathbf{x}^{(i-1)} \rVert < \epsilon\)
- (Relative) change of functional value: \(\frac{| f(\mathbf{x}^{(i)}) - f(\mathbf{x}^{(i-1)})|}{|f(\mathbf{x}^{(i)})|} < \epsilon\) or \(| f(\mathbf{x}^{(i)}) - f(\mathbf{x}^{(i-1)})| < \epsilon\)
- Stop at a pre-specified number of iterations
BFGS Demo
Second-order Newton’s Method
- Second order Taylor expansion at a current point \(\mathbf{x}\):
\[f(\mathbf{x}^\ast) \approx f(\mathbf{x}) + \nabla f(\mathbf{x})' (\mathbf{x}^\ast - \mathbf{x}) + \frac{1}{2} (\mathbf{x}^\ast - \mathbf{x})' \mathbf{H}(\mathbf{x}) (\mathbf{x}^\ast - \mathbf{x})\]
Take derivative w.r.t \(\mathbf{x}^\ast\) on both sides: \[0 = \nabla f(\mathbf{x}^\ast) = 0 + \nabla f(\mathbf{x}) + \mathbf{H}(\mathbf{x}) (\mathbf{x}^\ast - \mathbf{x})\] \[\boxed{\mathbf{x}^{(i+1)} = \mathbf{x}^{(i)} - \mathbf{H}(\mathbf{x}^{(i)})^{-1} \nabla f(\mathbf{x}^{(i)})}\]
For numerical stability, introduce a step size \(\delta \in (0, 1)\): \[\mathbf{x}^{(i+1)} = \mathbf{x}^{(i)} - {\color{red}{\delta}} \, \mathbf{H}(\mathbf{x}^{(i)})^{-1} \nabla f(\mathbf{x}^{(i)})\]
First-Order Gradient Descent
Note
When \(\mathbf{H}\) or \(\mathbf{H}^{-1}\) is difficult to compute
Get an approximate one in a computationally inexpensive way. The BFGS algorithm is such an approach by iteratively updating its (inverse) estimation.
Use first-order methods
- When using \(\mathbf{H}= \mathbf{I}\), we update \[\mathbf{x}^{(i+1)} = \mathbf{x}^{(i)} - \delta \nabla f(\mathbf{x}^{(i)}).\]
- It is crucial to figure out the step size \(\delta\).
- A too large \(\delta\) may not converge.
- A too small \(\delta\) takes too many iterations.
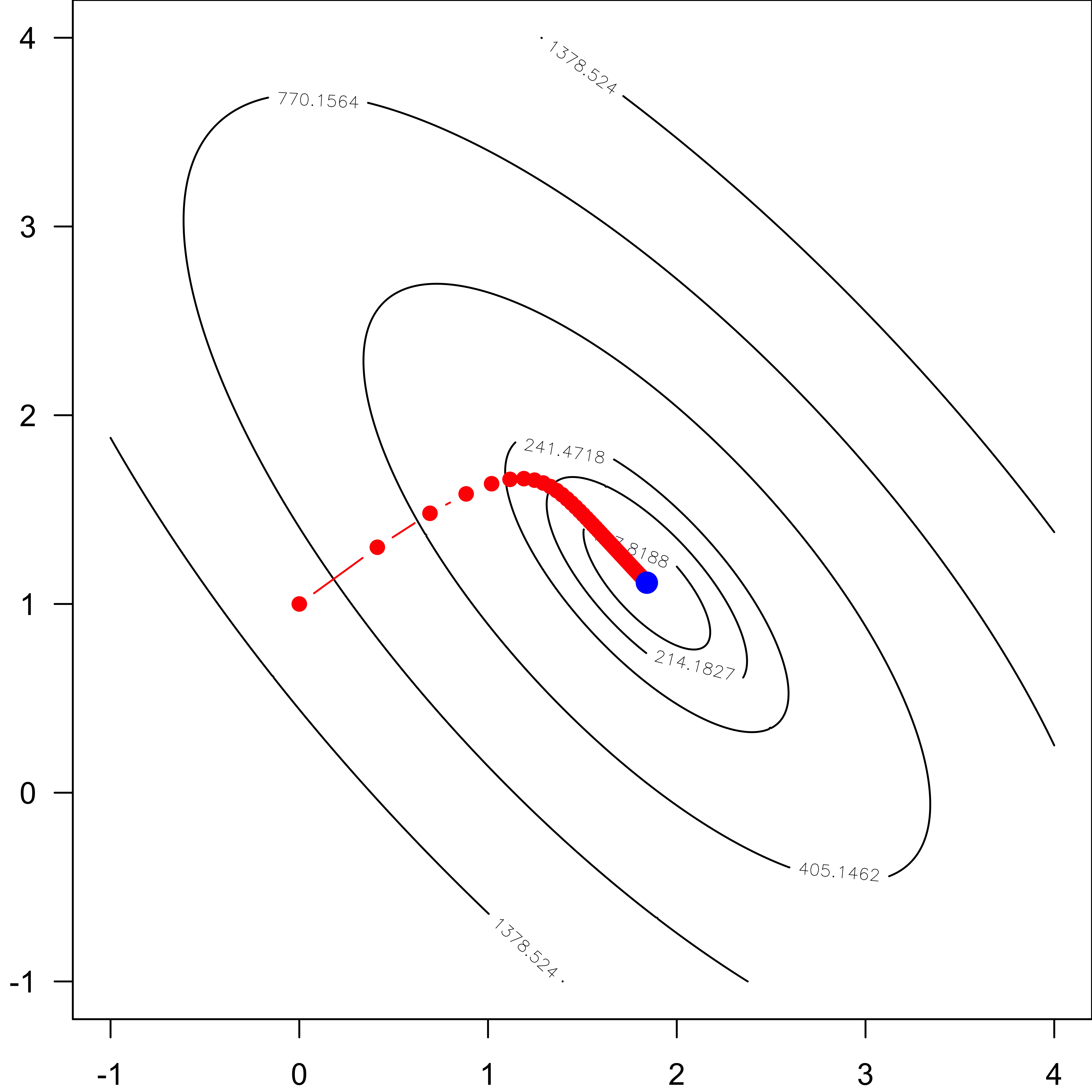
Demo \(SS_{res}\) Contour
The objective function is \(\ell(\boldsymbol \beta) = \frac{1}{2n}||\mathbf{y} - \mathbf{X} \boldsymbol \beta ||^2\) with solution \({\bf b} = \left(\mathbf{X}'\mathbf{X}\right)^{-1} \mathbf{X}'\mathbf{y}\).
Code
set.seed(2024)
n <- 200
# create some data with linear model
X <- MASS::mvrnorm(n, c(0, 0), matrix(c(1, 0.7, 0.7, 1), 2, 2))
y <- rnorm(n, mean = 2 * X[, 1] + X[, 2])
beta1 <- seq(-1, 4, 0.005)
beta2 <- seq(-1, 4, 0.005)
allbeta <- data.matrix(expand.grid(beta1, beta2))
rss <- matrix(apply(allbeta, 1,
function(b, X, y) sum((y - X %*% b) ^ 2), X, y),
length(beta1), length(beta2))
# quantile levels for drawing contour
quanlvl = c(0.01, 0.025, 0.05, 0.2, 0.5, 0.75)
# plot the contour
contour(beta1, beta2, rss, levels = quantile(rss, quanlvl), las = 1)
box()
# the truth
b <- solve(t(X) %*% X) %*% t(X) %*% y
points(b[1], b[2], pch = 19, col = "blue", cex = 2)
Demo Gradient Descent
\[ \begin{align} \frac{\partial \ell(\boldsymbol \beta)}{\partial \boldsymbol \beta} = -\frac{1}{n} \sum_{i=1}^n (y_i - x_i' \boldsymbol \beta) x_i. \end{align} \] First set an initial beta value, say \(\boldsymbol \beta = \mathbf{0}\) for all entries, then proceed with the update
\[\begin{align} \boldsymbol \beta^\text{new} =& \boldsymbol \beta^\text{old} - \delta \frac{\partial \ell(\boldsymbol \beta)}{\partial \boldsymbol \beta}\\ =&\boldsymbol \beta^\text{old} + \delta \frac{1}{n} \sum_{i=1}^n (y_i - x_i' \boldsymbol \beta) x_i.\\ \end{align}\]
Demo Gradient Descent
- Set \(\boldsymbol{\beta}^{(0)} = \mathbf{0}\), \(\delta = 0.2\)
Demo Effect of \(\delta\)

Revisit optim()
optim(par, fn, gr = NULL, ...,
method = c("Nelder-Mead", "BFGS", "CG", "L-BFGS-B", "SANN", "Brent"),
lower = -Inf, upper = Inf,
control = list(), hessian = FALSE)- If gradient is known, we provide this information in the argument
gr =to avoid numerically approximating the gradient.- faster convergence
- more precise
