Feature Selection and LASSO

MSSC 6250 Statistical Machine Learning

Dr. Cheng-Han Yu
Department of Mathematical and Statistical Sciences
Marquette University

Feature/Variable Selection

When OLS Doesn’t Work Well

When \(p \gg n\), it is often that many of the features in the model are not associated with the response.

• Model Interpretability: By removing irrelevant features \(X_j\)s, i.e., setting the corresponding \(\beta_j\)s to zero, we can obtain a model that is more easily interpreted. (Feature/Variable selection)

• Least squares is unlikely to yield any coefficient estimates that are exactly zero.

Variable Selection

• We have a large pool of candidate regressors, of which only a few are likely to be important.

Two “conflicting” goals in model building:

• as many features as possible for better predictive performance on new data (smaller bias).

• as few regressors as possible because as the number of regressors increases,

  • \(\mathrm{Var}(\hat{y})\) will increase (larger variance)
  • cost more in data collecting and maintaining
  • more model complexity

A compromise between the two hopefully leads to the “best” regression equation.

What does best mean?

There is no unique definition of “best”, and different methods specify different subsets of the candidate regressors as best.

Three Classes of Methods

• Subset Selection (ISL Sec. 6.1) Identify a subset of the \(p\) predictors that we believe to be related to the response.
  • Need a selection method and a selection criterion.
• Shrinkage (ISL Sec. 6.2) Fit a model that forces some coefficients to be shrunk to zero.
  • Lasso glmnet::glmnet()
• Dimension Reduction (ISL Sec. 6.3) Find \(m\) representative features that are linear combinations of the \(p\) original predictors (\(m \ll p\)), then fit least squares.
  • Principal component regression (Unsupervised) pls::pcr()
  • Partial least squares (Supervised) pls::plsr()

Subset Selection

• MSSC 5780 slides and ISL Sec. 6.1

• Identify a subset of all the candidate predictors with the best OLS performance.
  • Best subset selection olsrr::ols_step_best_subset()
  • Forward stepwise selection olsrr::ols_step_forward_p()
  • Backward stepwise elimination olsrr::ols_step_backward_p()
  • Hybrid stepwise selection olsrr::ols_step_both_p()

We then fit a model using least squares on the reduced set of variables.

Selection Criteria

• An evaluation metric should consider Goodness of Fit and Model Complexity:

Goodness of Fit: The more regressors, the better

Complexity Penalty: The less regressors, the better

• Evaluate subset models:
  • \(R_{adj}^2\) \(\uparrow\)
  • Mallow’s \(C_p\) \(\downarrow\)
  • Information Criterion (AIC, BIC) \(\downarrow\)
  • PREdiction Sum of Squares (PRESS) \(\downarrow\) (Allen, D.M. (1974))

Note

All the measures are not appropriate in the high-dimensional (\(n \ll p\)) setting. - Indirectly estimate test error by making adjustment to the training error to account for the bias due to overfitting. - Directly estimate test error using CV.

Lasso (Least Absolute Shrinkage and Selection Operator)

Why Lasso?

• Subset selection methods

  • may be computationally infeasible (fit OLS over millions of times)
  • do not explore all possible subset models (no global solution)

• Ridge regression does shrink coefficients, but still include all predictors.

• Lasso regularizes coefficients so that some coefficients are shrunk to zero, doing feature selection.

• Like ridge regression, for a given \(\lambda\), Lasso only fits a single model.

Ridge OK for prediction, but bad at interpretation

What is Lasso?

Different from the Ridge regression that adds \(\ell_2\) norm, Lasso adds \(\ell_1\) penalty on the parameters:

\[\begin{align} \widehat{\boldsymbol \beta}^\text{l} =& \, \, \mathop{\mathrm{arg\,min}}_{\boldsymbol \beta} \lVert \mathbf{y}- \mathbf{X}\boldsymbol \beta\rVert_2^2 + n \lambda \lVert\boldsymbol \beta\rVert_1\\ =& \, \, \mathop{\mathrm{arg\,min}}_{\boldsymbol \beta} \frac{1}{n} \sum_{i=1}^n (y_i - x_i' \boldsymbol \beta)^2 + \lambda \sum_{j=1}^p |\beta_j|, \end{align}\]

• The \(\ell_1\) penalty forces some of the coefficient estimates to be exactly equal to zero when \(\lambda\) is sufficiently large, yielding sparse models.

\(\ell_2\) vs. \(\ell_1\)

• Ridge shrinks big coefficients much more than lasso.
• Lasso has larger penalty on small coefficients.

• Ridge shrinks big coefficients much more than lasso.
• Lasso has larger penalty on small coefficients. This is one of the intuitions why Lasso has exact zero coefficients after shrinkage. Because when punishing small coefficients a lot more, it may be better to set them exactly equal to zero to get smaller loss or objective value.

ElemStatLearn::prostate Data

lcavol	lweight	age	lbph	svi	lcp	gleason	pgg45	lpsa	train
-0.580	2.77	50	-1.386	0	-1.39	6	0	-0.431	TRUE
-0.994	3.32	58	-1.386	0	-1.39	6	0	-0.163	TRUE
-0.511	2.69	74	-1.386	0	-1.39	7	20	-0.163	TRUE
-1.204	3.28	58	-1.386	0	-1.39	6	0	-0.163	TRUE
0.751	3.43	62	-1.386	0	-1.39	6	0	0.372	TRUE
-1.050	3.23	50	-1.386	0	-1.39	6	0	0.765	TRUE
0.737	3.47	64	0.615	0	-1.39	6	0	0.765	FALSE
0.693	3.54	58	1.537	0	-1.39	6	0	0.854	TRUE

cv.glmnet(alpha = 1)

lasso_fit <- cv.glmnet(x = data.matrix(prostate[, 1:8]), y = prostate$lpsa, nfolds = 10, 
                       alpha = 1)

    plot(lasso_fit)
    plot(lasso_fit$glmnet.fit, "lambda")

genridge Package

Lasso Coefficients

• lambda.min contains more nonzero coefficients.

• Larger penalty \(\lambda\) forces more coefficients to be zero, and the model is more “sparse”.

coef(lasso_fit, s = "lambda.min")

9 x 1 sparse Matrix of class "dgCMatrix"
                  s1
(Intercept)  0.17999
lcavol       0.56099
lweight      0.61908
age         -0.02069
lbph         0.09531
svi          0.75180
lcp         -0.09912
gleason      0.04745
pgg45        0.00432

coef(lasso_fit, s = "lambda.1se")

9 x 1 sparse Matrix of class "dgCMatrix"
               s1
(Intercept) 0.644
lcavol      0.455
lweight     0.314
age         .    
lbph        .    
svi         0.367
lcp         .    
gleason     .    
pgg45       .    

One-Variable Lasso and Shrinkage: Concept

• Lasso solution does not have an analytic or closed form in general.

• Consider the univariate regression model

\[\underset{\beta}{\mathop{\mathrm{arg\,min}}} \quad \frac{1}{n} \sum_{i=1}^n (y_i - x_i \beta)^2 + \lambda |\beta|\]

With some derivation, and also utilize the OLS solution of the loss function, we have

\[\begin{align} &\frac{1}{n} \sum_{i=1}^n (y_i - x_i \beta)^2 \\ =& \frac{1}{n} \sum_{i=1}^n (y_i - x_i b + x_i b - x_i \beta)^2 \\ =& \frac{1}{n} \sum_{i=1}^n \Big[ \underbrace{(y_i - x_i b)^2}_{\text{I}} + \underbrace{2(y_i - x_i b)(x_i b - x_i \beta)}_{\text{II}} + \underbrace{(x_i b - x_i \beta)^2}_{\text{III}} \Big] \end{align}\]

One-Variable Lasso and Shrinkage: Concept

\[\begin{align} & \sum_{i=1}^n 2(y_i - x_i b)(x_i b - x_i \beta) = (b - \beta) {\color{OrangeRed}{\sum_{i=1}^n 2(y_i - x_i b)x_i}} = (b - \beta) {\color{OrangeRed}{0}} = 0 \end{align}\]

Our original problem reduces to just the third term and the penalty

\[\begin{align} &\underset{\beta}{\mathop{\mathrm{arg\,min}}} \quad \frac{1}{n} \sum_{i=1}^n (x_ib - x_i \beta)^2 + \lambda |\beta| \\ =&\underset{\beta}{\mathop{\mathrm{arg\,min}}} \quad \frac{1}{n} \left[ \sum_{i=1}^n x_i^2 \right] (b - \beta)^2 + \lambda |\beta| \end{align} \] Without loss of generality, assume that \(x\) is standardized with mean 0 and variance \(\frac{1}{n}\sum_{i=1}^n x_i^2 = 1\).

b is arbitrary We learned that to solve for an optimizer, we can set the gradient to be zero. However, the function is not everywhere differentiable

One-Variable Lasso and Shrinkage: Concept

This leads to a general problem of

\[\underset{\beta}{\mathop{\mathrm{arg\,min}}} \quad (\beta - b)^2 + \lambda |\beta|,\] For \(\beta > 0\),

\[\begin{align} 0 =& \frac{\partial}{\partial \beta} \,\, \left[(\beta - b)^2 + \lambda |\beta| \right] = 2 (\beta - b) + \lambda \\ \Longrightarrow \quad \beta =&\, b - \lambda/2 \end{align}\]

\[\begin{align} \widehat{\beta}^\text{l} &= \begin{cases} b - \lambda/2 & \text{if} \quad b > \lambda/2 \\ 0 & \text{if} \quad |b| \le \lambda/2 \\ b + \lambda/2 & \text{if} \quad b < -\lambda/2 \\ \end{cases} \end{align}\]

• Lasso provides a soft-thresholding solution.

• When \(\lambda\) is large enough, \(\widehat{\beta}^\text{l}\) will be shrunk to zero.

b is arbitrary We learned that to solve for an optimizer, we can set the gradient to be zero. However, the function is not everywhere differentiable

Objective function

The objective function is \((\beta - 1)^2\). Once the penalty is larger than 2, the optimizer would stay at 0.

Based on our analysis, once the penalty is larger than 2, the optimizer would stay at 0.

Variable Selection Property and Shrinkage

• The proportion of times a variable has a non-zero parameter estimation.

• \(\mathbf{y}= \mathbf{X}\boldsymbol \beta + \epsilon = \sum_{j = 1}^p X_j \times 0.4^{\sqrt{j}} + \epsilon\)

• \(p = 20\), \(\epsilon \sim N(0, 1)\) and replicate 100 times.

• Since Lasso shrinks some parameter to exactly zero, it has the variable selection property — the ones that are nonzero are the ones being selected. This is a very nice properly in high-dimensional data analysis, where we cannot estimate the effects of all variables.

• We can then look at the proportion of times a variable has a non-zero parameter estimation

Bias-Variance Trade-off

Comparing Lasso and Ridge

Constrained Optimization

• For every value of \(\lambda\), there is some \(s\) such that the two optimization problems are equivalent, giving the same coefficient estimates.

• The \(\ell_1\) and \(\ell_2\) penalties form a constraint region that \(\beta_j\) can move around or budget for how large \(\beta_j\) can be.

• Larger \(s\) (smaller \(\lambda\)) means a larger region \(\beta_j\) can freely move.

Lasso \[\begin{align} \min_{\boldsymbol \beta} \,\,& \lVert \mathbf{y}- \mathbf{X}\boldsymbol \beta\rVert_2^2 + n\lambda\lVert\boldsymbol \beta\rVert_1 \end{align}\]

\[\begin{align} \min_{\boldsymbol \beta} \,\,& \lVert \mathbf{y}- \mathbf{X}\boldsymbol \beta\rVert_2^2\\ \text{s.t.} \,\, & \sum_{j=1}^p|\beta_j| \leq s \end{align}\]

Ridge \[\begin{align} \min_{\boldsymbol \beta} \,\,& \lVert \mathbf{y}- \mathbf{X}\boldsymbol \beta\rVert_2^2 + n\lambda\lVert\boldsymbol \beta\rVert_2^2 \end{align}\]

\[\begin{align} \min_{\boldsymbol \beta} \,\,& \lVert \mathbf{y}- \mathbf{X}\boldsymbol \beta\rVert_2^2\\ \text{s.t.} \,\, & \sum_{j=1}^p \beta_j^2 \leq s \end{align}\]

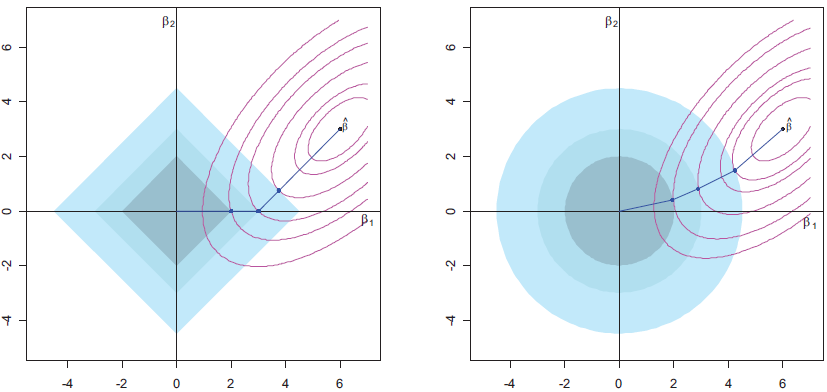
Geometric Representation of Optimization

What do the constraints look like geometrically?

When \(p = 2\),

• the \(\ell_1\) constraint is \(|\beta_1| + |\beta_2| \leq s\) (diamond)
• the \(\ell_2\) constraint is \(\beta_1^2 + \beta_2^2 \leq s\) (circle)

Source: https://stats.stackexchange.com/questions/350046/the-graphical-intuiton-of-the-lasso-in-case-p-2

the solution has to stay within the shaded area. The objective function is shown with the contour, and once the contained area is sufficiently small, some β parameter will be shrunk to exactly zero. On the other hand, the Ridge regression also has a similar interpretation. However, since the constrained areas is a circle, it will never for the estimated parameters to be zero.

Way of Shrinking (\(p = 1\) and standardized \(x\))

Lasso Soft-thresholding

\[\begin{align} \widehat{\beta}^\text{l} &= \begin{cases} b - \lambda/2 & \text{if} \quad b > \lambda/2 \\ 0 & \text{if} \quad |b| < \lambda/2 \\ b + \lambda/2 & \text{if} \quad b < -\lambda/2 \\ \end{cases} \end{align}\]

Ridge Proportional shrinkage

\[\begin{align} \widehat{\beta}^\text{r} = \dfrac{b}{1+\lambda}\end{align}\]

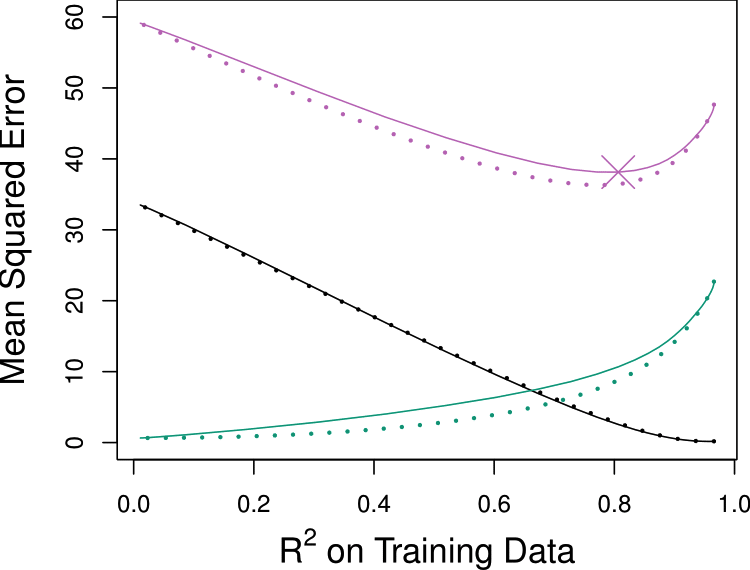
Predictive Performance

Perform well (lower test MSE) when

Lasso (—)

• A relatively small number of \(\beta_j\)s are substantially large, and the remaining \(\beta_k\)s are small or equal to zero.

• Reduce more bias

ISL Fig. 6.9

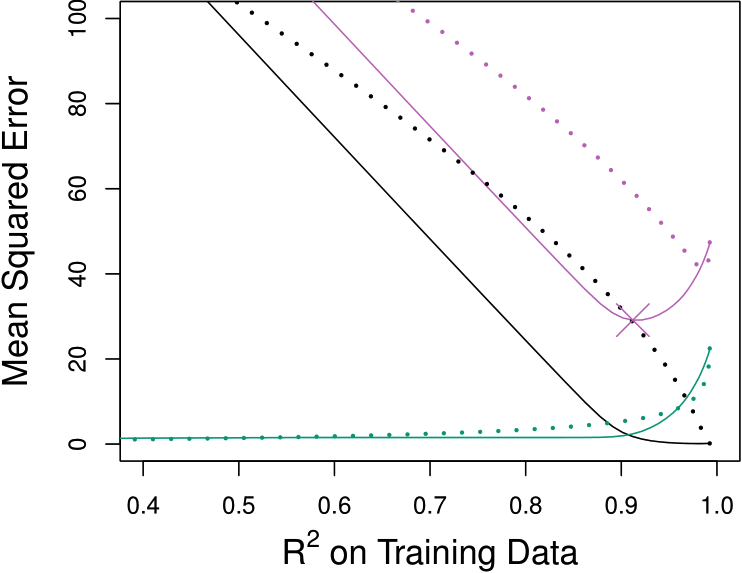
Ridge (\(\cdots\cdots\))

• The response is a function of many predictors, all with coefficients of roughly equal size.

• Reduce more variance

ISL Fig. 6.8

Ridge focus more on variance stablization Lasso focus more on model selection and interpretbility higher R^2 (larger lambda), more overfitting, so low bias high variance

Notes of Lasso

Warning

• Even Lasso does feature selection, do not add predictors that are known to be not associated with the response in any way.

• Curse of dimensionality. The test MSE tends to increase as the dimensionality \(p\) increases, unless the additional features are truly associated with the response.

• Do not conclude that the predictors with non-zero coefficients selected by Lasso and other selection methods predict the response more effectively than other predictors not included in the model.

This is just one of many possible models for predicting response, and that it must be further validated on independent data sets.

Other Topics

• Combination \(\ell_1\) and \(\ell_2\): Elastic net penalty (Zou and Hastie, 2005)

\[\lambda \left[ (1 - \alpha) \lVert \boldsymbol \beta\rVert_2^2 + \alpha \lVert\boldsymbol \beta\lVert_1 \right]\]

• General \(\ell_q\) penalty: \(\lambda \sum_{j=1}^p |\beta_j|^q\)

ESL Fig. 3.12

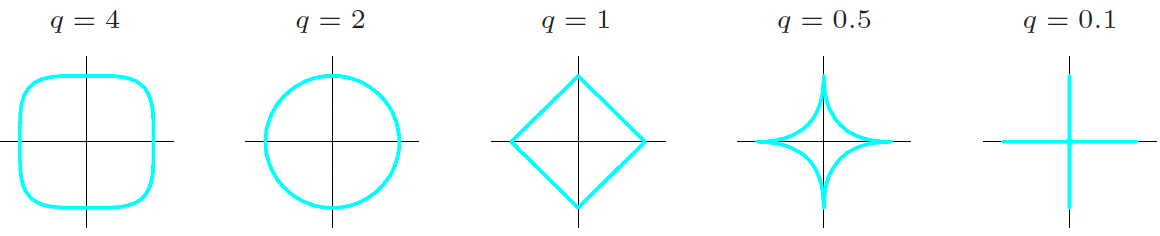
Other Topics

• Algorithms
  • Shooting algorithm (Fu 1998)
  • Least angle regression (LAR) (Efron et al. 2004)
  • Coordinate descent (Friedman et al 2010) (used in glmnet)

• Variants
  • Adaptive Lasso
  • Group Lasso
  • Bayesian Lasso, etc.

Lasso may suffer in the case where two variables are strongly correlated. The situation is similar to OLS, however, in Lasso, it would only select one out of the two, instead of letting both parameter estimates to be large. This is not preferred in some practical situations such as genetic studies because expressions of genes from the same pathway may have large correlation, but biologist want to identify all of them instead of just one. The Ridge penalty may help in this case because it naturally considers the correlation structure. The following simulation may show the effect. - The Lasso problem is convex, although it may not be strictly convex in β when p is large - The solution is a global minimum, but may not be the unique global one - The Lasso solution is unique under conditions of the covariance matrix