Logistic Regression

MSSC 6250 Statistical Machine Learning

Dr. Cheng-Han Yu
Department of Mathematical and Statistical Sciences
Marquette University

Binary Logistic Regression

Non-Gaussian and Non-continuous Response

• In many applications, the response or error term are nonnormal.

  • Binary response: how an online banking system determine whether or not a transaction is fraudulent based on the user’s IP address.
  • Count response: how weather conditions affect the number of users of a bike sharing program during a particular hour of the day.

• Besides normal, the response in a generalized linear model (GLM) can be Bernoulli, binomial, Poisson, etc.

• There is no assumption that \(\mathrm{Var}(y_i)\) is homogeneous: Both \(E(y_i)\) and \(\mathrm{Var}(y_i)\) may vary with the regressors from data point to data point.

• Ordinary least squares does not apply when the response is not normal.

Classification

• Linear regression assumes that the response \(Y\) is numerical.
• In many situations, \(Y\) is categorical.

• A process of predicting categorical response is known as classification.

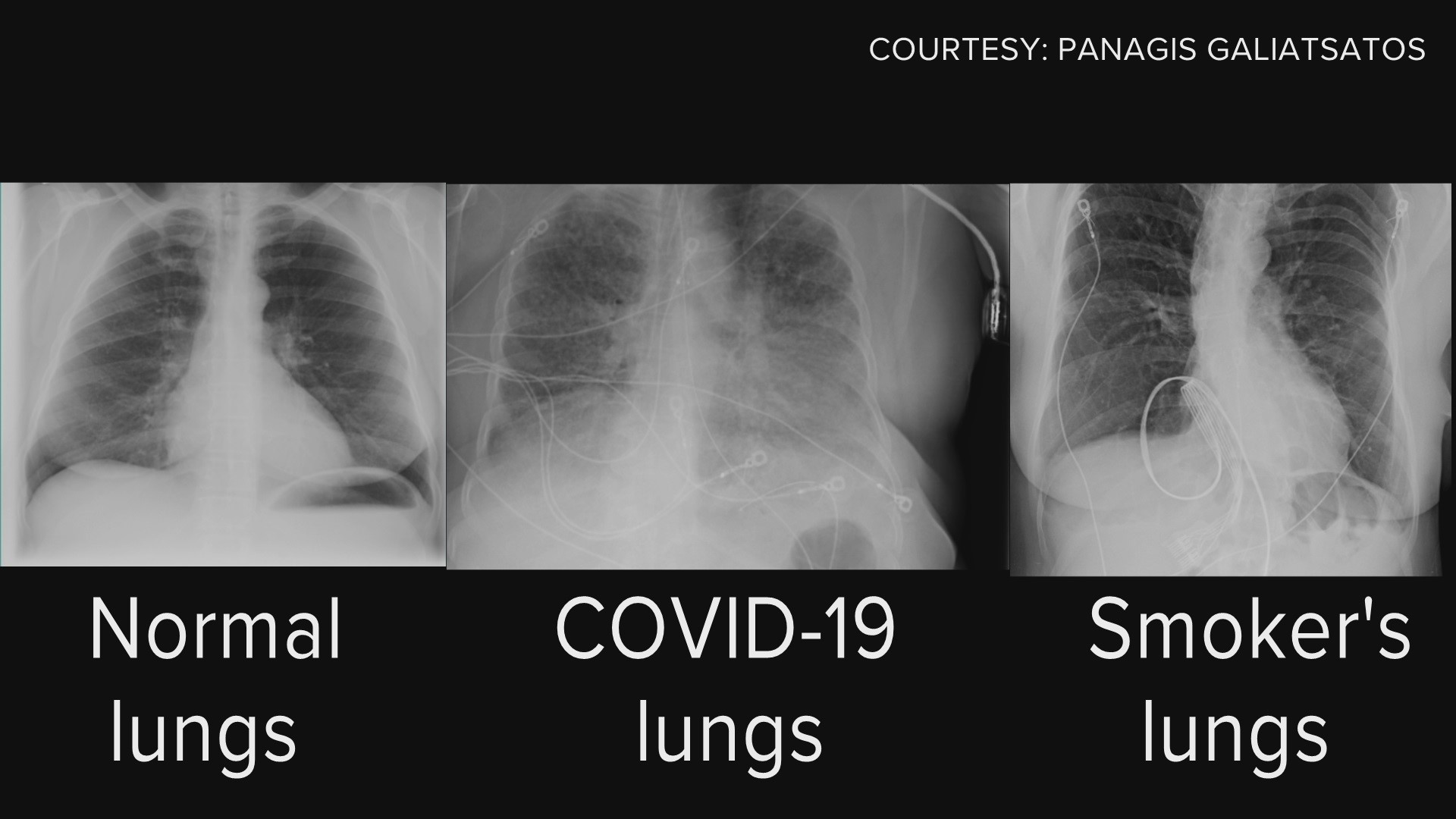
Normal vs. COVID vs. Smoking

fake news vs. true news

Regression Function \(f(x)\) vs. Classifier \(C(x)\)

https://daviddalpiaz.github.io/r4sl/classification-overview.html

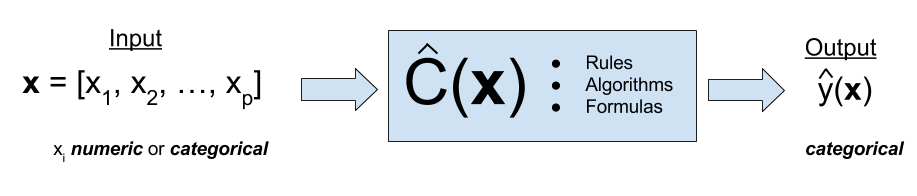
Soft and Hard Classifiers

Two popular approaches when modeling binary data

• Soft classifiers
  • Estimate the conditional probabilities \(Pr(Y = k \mid {\bf X})\) for each category \(k\).
  • Use \(\mathbf{1}\{Pr(Y \mid {\bf X}) > c \}\) for classification, where \(c \in(0, 1)\) is a threshold or cutoff.
  • e.g. logistic regression

• Hard classifiers
  • Directly estimate the classification decision boundary
  • e.g. support vector machines

Classification Example

Given the training data \(\{(x_i, y_i)\}_{i=1}^n\), we build a classifier to predict whether people will default on their credit card payment \((Y)\) yes or no, based on monthly credit card balance \((X)\).

Why Not Linear Regression

\[Y =\begin{cases} 0 & \quad \text{if not default}\\ 1 & \quad \text{if default} \end{cases}\]

• \(Y = \beta_0 + \beta_1X + \epsilon\), \(\, X =\) credit card balance

What are potential issues with this dummy variable approach?

• \(\hat{Y} = b_0 + b_1X\) estimates \(P(Y = 1 \mid X) = P(default = yes \mid balance)\), which is equivalent to linear discriminant analysis (LDA) discussed later.

• However,

Why Not Linear Regression?

• Probability estimates can be outside \([0, 1]\).

Why Not Linear Regression?

• Linear regression generally cannot handle more than two categories.

\[Y =\begin{cases} 1 & \quad \text{stroke}\\ 2 & \quad \text{drug overdose} \\ 3 & \quad \text{epileptic seisure} \end{cases}\]

• The coding

  • suggests an ordering epileptic seisure \(>\) drug overdose \(>\) stroke
  • implies that stroke \(-\) drug overdose \(=\) drug overdose \(-\) epileptic seizure.

Binary Logistic Regression

• First predict the probability of each category of \(Y\)
• Predict probability of default using a S-shaped curve.

Framing the Problem: Binary Responses

We use normal distribution for numerical \(y\). What distribution we can use for binary \(y\) that takes value 0 or 1?

• Each outcome default \((y = 1)\) and not default \((y = 0)\) is a Bernoulli variable. But,

• The probability of “success” \(\pi\) is not constant but varies with predictor values!

\[ y_i \mid x_i \stackrel{indep}{\sim} \text{Bernoulli}(\pi_i = \pi(x_i)) = \text{binomial}(m=1,\pi = \pi_i) \]

• \(X =\) balance. \(x_1 = 2000\) has a larger \(\pi_1 = \pi(2000)\) than \(\pi_2 = \pi(500)\) with \(x_2 = 500\)
• Credit cards with a higher balance are more likely to be defaulted.

In the credit card example, - do we have exactly two outcomes? - do we have constant probability? \(P(y_1 = 1) = P(y_2 = 1) = \cdots = P(y_n = 1) = \pi?\) Exactly the same idea as linear regression, where the the mean response is not constant but varies with the value of predictors, \(E(y_i) = \beta_0+\beta_1x_i\).

Logistic Function

Instead of predicting \(y_i\) directly, we use the predictors to model its probability of success, \(\pi_i\).

But how?

• Transform \(\pi \in (0, 1)\) into a variable \(\eta \in (-\infty, \infty)\). Then construct a linear predictor on \(\eta\): \(\eta_i = \mathbf{x}_i'\boldsymbol \beta\)

• Logit function: For \(0 < \pi < 1\)

\[\eta = \text{logit}(\pi) = \ln\left(\frac{\pi}{1-\pi}\right)\]

Logit function \(\eta = \text{logit}(\pi) = \ln\left(\frac{\pi}{1-\pi}\right)\)

Logistic Function

• The logit function \(\eta = \text{logit}(\pi) = \ln\left(\frac{\pi}{1-\pi}\right)\) takes a value \(\pi \in (0, 1)\) and maps it to a value \(\eta \in (-\infty, \infty)\).
• Logistic function: \[\pi = \text{logistic}(\eta) = \frac{1}{1+\exp(-\eta)} \in (0, 1)\]
• The logistic (sigmoid) function takes a value \(\eta \in (-\infty, \infty)\) and maps it to a value \(\pi \in (0, 1)\).

• Once \(\eta\) is estimated by the linear regression, we use the logistic function to transform \(\eta\) back to the probability.

\[\pi = \text{logistic}(\eta) = \frac{\exp(\eta)}{1+\exp(\eta)} = \frac{1}{1+\exp(-\eta)} \in (0, 1)\]

Logistic (Sigmoid) Function \(\pi = \text{logistic}(\eta) = \frac{1}{1+\exp(-\eta)}\)

Logistic Regression Model

For \(i = 1, \dots, n\) and with \(p\) predictors: \[Y_i \mid \pi_i({\bf x}_i) \stackrel{indep}{\sim} \text{Bernoulli}(\pi_i), \quad {\bf x}_i' = (x_{i1}, \dots, x_{ip})\] \[\text{logit}(\pi_i) = \ln \left( \frac{\pi_i}{1 - \pi_i} \right) = \eta_i = \beta_0+\beta_1 x_{i1} + \cdots + \beta_p x_{ip} = {\bf x}_i'\boldsymbol \beta\]

• The \(\eta_i = \text{logit}(\pi_i)\) is a link function that links the linear predictor and the mean of \(Y_i\).

\[\small E(Y_i) = \pi_i = \frac{1}{1 + \exp(-{\bf x}_i'\boldsymbol \beta)}\] \[\small \hat{\pi}_i = \frac{1}{1 + \exp(-{\bf x}_i'\hat{\boldsymbol \beta} )}\]

Default Data in ISLR2

data("Default"); head(Default, 10)

   default student balance income
1       No      No     730  44362
2       No     Yes     817  12106
3       No      No    1074  31767
4       No      No     529  35704
5       No      No     786  38463
6       No     Yes     920   7492
7       No      No     826  24905
8       No     Yes     809  17600
9       No      No    1161  37469
10      No      No       0  29275

str(Default)

'data.frame':   10000 obs. of  4 variables:
 $ default: Factor w/ 2 levels "No","Yes": 1 1 1 1 1 1 1 1 1 1 ...
 $ student: Factor w/ 2 levels "No","Yes": 1 2 1 1 1 2 1 2 1 1 ...
 $ balance: num  730 817 1074 529 786 ...
 $ income : num  44362 12106 31767 35704 38463 ...

glm()

logit_fit <- glm(default ~ balance, data = Default, 
                 family = binomial)
coef(summary(logit_fit))

            Estimate Std. Error z value Pr(>|z|)
(Intercept) -10.6513    0.36116     -29 3.6e-191
balance       0.0055    0.00022      25 2.0e-137

\(\hat{\eta} = \text{logit}(\hat{\pi}) = \ln \left( \frac{\hat{\pi}}{1 - \hat{\pi}}\right) = -10.65 + 0.0055 \times \text{balance}\)

Interpretation of Coefficients

The ratio \(\frac{\pi}{1-\pi} \in (0, \infty)\) is called the odds of some event.

• Example: If 1 in 5 people will default, the odds is 1/4 since \(\pi = 0.2\) implies an odds of \(0.2/(1−0.2) = 1/4\).

\[\ln \left( \frac{\pi(x)}{1 - \pi(x)} \right)= \beta_0 + \beta_1x\]

• Increasing \(x\) by one unit
  • changes the log-odds by \(\beta_1\)
  • multiplies the odds by \(e^{\beta_1}\)

• \(\beta_1\) does not correspond to the change in \(\pi(x)\) associated with a one-unit increase in \(x\).
• \(\beta_1\) is the change in log odds associated with one-unit increase in \(x\).

Interpretation of Coefficients

            Estimate Std. Error z value Pr(>|z|)
(Intercept)  -10.651       0.36     -29        0
balance        0.005       0.00      25        0

• \(\hat{\eta} = \text{logit}(\hat{\pi}) = \ln \left( \frac{\hat{\pi}}{1 - \hat{\pi}}\right) = -10.65 + 0.0055 \times \text{balance}\)

• \(\hat{\eta}(x) = \hat{\beta}_0 + \hat{\beta}_1x\)
• \(\hat{\eta}(x+1) = \hat{\beta}_0 + \hat{\beta}_1(x+1)\)
• \(\hat{\eta}(x+1) - \hat{\eta}(x) = \hat{\beta}_1 = \ln(\text{odds}_{x+1}) - \ln(\text{odds}_{x})\)
• One-unit increase in balance increases the log odds of default by 0.005 units.

• The odds ratio, \(\widehat{OR} = \frac{\text{odds}_{x+1}}{\text{odds}_{x}} = e^{\hat{\beta}_1} = e^{0.0055} = 1.005515\).
• The odds of default increases by 0.5% with additional one unit of credit card balance.

Pr(default) When Balance is 2000

\[\log\left(\frac{\hat{\pi}}{1-\hat{\pi}}\right) = -10.65+0.0055\times 2000\]

\[ \hat{\pi} = \frac{1}{1+\exp(-(-10.65+0.0055 \times 2000)} = 0.586\]

pi_hat <- predict(logit_fit, type = "response")
eta_hat <- predict(logit_fit, type = "link")  ## default gives us b0 + b1*x
predict(logit_fit, newdata = data.frame(balance = 2000), type = "response")

   1 
0.59 

Probability Curve

What is the probability of default when the balance is 500? What about balance 2500?

• 500 balance: Pr(default) = 0
• 2000 balance: Pr(default) = 0.59
• 2500 balance: Pr(default) = 0.96

Maximum Likelihood Estimation

• glm() uses maximum likelihood to estimate the parameters \(\boldsymbol \beta\).

The log-likelihood is given by

\[\ell(\boldsymbol \beta) = \sum_{i=1}^n \log \, p(y_i \mid x_i, \boldsymbol \beta).\]

Using Bernoulli probabilities, we have

\[\begin{align} \ell(\boldsymbol \beta) =& \sum_{i=1}^n \log \left\{ \pi(\mathbf{x}_i)^{y_i} [1-\pi(\mathbf{x}_i)]^{1-y_i} \right\}\\ =& \sum_{i=1}^n y_i \log \frac{\pi(\mathbf{x}_i)}{1-\pi(\mathbf{x}_i)} + \log [1-\pi(\mathbf{x}_i)] \\ =& \sum_{i=1}^n y_i \mathbf{x}_i' \boldsymbol \beta- \log [ 1 + \exp(\mathbf{x}_i' \boldsymbol \beta)] \end{align}\]

Maximum Likelihood Estimation

• We can use Newton’s method that needs the gradient and Hessian matrix.

\[\boldsymbol \beta^{\text{new}} = \boldsymbol \beta^{\text{old}} - \left[ \frac{\partial ^2 \ell(\boldsymbol \beta)}{\partial \boldsymbol \beta\partial \boldsymbol \beta'}\right] ^{-1}\frac{\partial \ell(\boldsymbol \beta)}{\partial \boldsymbol \beta}\]

• Simply use optim()

x <- as.matrix(cbind("intercept" = 1, Default$balance))
y <- as.matrix(as.numeric(Default$default) - 1)
beta <- rep(0, ncol(x))  ## start with 0

optim(beta, fn = my_loglik, gr = my_gradient, method = "BFGS", 
      x = x, y = y, 
      control = list("fnscale" = -1))$par # "fnscale" = -1 for maximization

[1] -10.6454   0.0055

Evaluation¹

• Confusion Matrix

	True 0	True 1
Predict 0	True Negative (TN)	False Negative (FN)
Predict 1	False Positive (FP)	True Positive (TP)

• Sensitivity (True Positive Rate) \(= P( \text{predict 1} \mid \text{true 1}) = \frac{TP}{TP+FN}\)

• Specificity (True Negative Rate) \(= P( \text{predict 0} \mid \text{true 0}) = \frac{TN}{FP+TN}\)

• Accuracy \(= \frac{TP + TN}{TP+FN+FP+TN} = \frac{1}{m}\sum_{j=1}^mI(y_j = \hat{y}_j)\), where \(y_j\)s are true test labels and \(\hat{y}_j\)s are their corresponding predicted label.

A good classifier is one which the test accuracy rate is highest, or test error rate \(\frac{1}{m}\sum_{j=1}^mI(y_j \ne \hat{y}_j)\) is smallest.

1. More on Wiki page.

Confusion Matrix

pred_prob <- predict(logit_fit, type = "response")
table(pred_prob > 0.5, Default$default)

       
          No  Yes
  FALSE 9625  233
  TRUE    42  100

• Packages:
  • caret (Classification And REgression Training)
  • yardstick of tidymodels

caret::confusionMatrix()
yardstick::conf_mat()

Receiver Operating Characteristic (ROC) Curve

• The ROC curve plots True Positive Rate (Sensitivity) vs. False Positive Rate (1 - Specificity)

• Packages: ROCR, pROC, yardstick::roc_curve()

library(ROCR)

# create an object of class prediction 
pred <- ROCR::prediction(
    predictions = pred_prob, 
    labels = Default$default)

# calculates the ROC curve
roc <- ROCR::performance(
    prediction.obj = pred, 
    measure = "tpr",
    x.measure = "fpr")

plot(roc, colorize = TRUE, lwd = 3)

Area Under Curve (AUC)

Find the area under the curve:

## object of class 'performance'
auc <- ROCR::performance(
    prediction.obj = pred, 
    measure = "auc")
auc@y.values

[[1]]
[1] 0.95

Threshold 0.5 Issue

• Threshold 0.5 may be inappropriate if
  • imbalanced data or skewed class distribution in training
  • the cost of one type of misclassification is more important than another.

Optimal Threshold

From the training set, choose the cut-off that maximizes

• G-Mean \(= \sqrt{\text{TPR} * \text{TNR}}\) (geometric mean of TPR and TNR)

• Youden’s J index \(= \text{TPR} + \text{TNR} - 1\) (the distance to the 45 degree identity line)

that minimizes

\(\sqrt{(1 - \text{TPR})^2 + (1 - \text{TNR})^2}\) (the distance to the optimal point)

Optimal Threshold

With Youden’s J index, the optimal threshold is \(3.18\%\).

• The predicted probabilities are not calibrated, e.g. those predicted by an SVM or decision tree.
• The metric used to train the model is different from the metric used to evaluate a final model.
• The class distribution is severely skewed.
• The cost of one type of misclassification is more important than another type of misclassification.
• Learning from Imbalanced Data Sets 1st ed. 2018 Edition
• https://machinelearningmastery.com/threshold-moving-for-imbalanced-classification/ The index is represented graphically as the height above the chance line, and it is also equivalent to the area under the curve subtended by a single operating point. https://web.expasy.org/pROC/files/pROC_1.7.2_R_manual.pdf

Multinomial Logistic Regression

Multinomial Logistic Regression

• When classifying \(K > 2\) categories, we can consider multinomial logistic regression¹.

• The response should be nominal. If \(Y_i\) is ordinal, we should consider the ordinal regression.

1. Sometimes it is known as multiclass logistic regression.

Multinomial Link

• First select a single class to serve as the baseline, the \(K\)th class for example.¹

\[Pr(Y = k \mid {\bf x}) = \dfrac{e^{\beta_{k0}+\beta_{k1}x_1 + \cdots + \beta_{kp}x_p}}{ \sum_{l=1}^{K}e^{\beta_{l0}+\beta_{l1}x_1 + \cdots + \beta_{lp}x_p}}\] for \(k = 1, 2, \dots, K-1\), and \[Pr(Y = K \mid {\bf x}) = \dfrac{1}{ \sum_{l=1}^{K}e^{\beta_{l0}+\beta_{l1}x_1 + \cdots + \beta_{lp}x_p}}.\]

For \(k = 1, \dots, K-1\), \[\log\left( \frac{Pr(Y = k \mid \mathbf{x})}{Pr(Y = K \mid \mathbf{x})} \right) = \beta_{k0}+\beta_{k1}x_1 + \cdots + \beta_{kp}x_p.\]

1. The coefficient estimates will differ if a different baseline is used. But the fitted values, predictions, log odds between any pair of classes remain the same.

Multinomial Link

• First select a single class to serve as the baseline, the \(K\)th class for example.¹

• \(\pi_{ik} = Pr(Y_i = k \mid {\bf x}_i)\): the probability that the \(i\)-th response falls in the \(k\)-th category.

• \(\sum_{k = 1}^K \pi_{ik} = 1\) for each observation \(i\).

• For \(k = 1, \dots, K-1\), the link \(\eta_{ik} = \log\left( \frac{\pi_{ik}}{\pi_{iK}}\right) = \beta_{k0}+\beta_{k1}x_1 + \cdots + \beta_{kp}x_p = {\bf x}_i'\boldsymbol \beta_k\), where \(\boldsymbol \beta_k = (\beta_{k0}, \beta_{k1}, \dots, \beta_{kp})'\)

What is the value of \(\eta_{iK}\)?

For \(k = 1, \dots, K\),

\[\pi_{ik} = \dfrac{e^{\eta_{ik}}}{\sum_{l=1}^{K}e^{\eta_{il}}}; \left(\pi_{iK} = \dfrac{1}{\sum_{l=1}^{K}e^{\eta_{il}}} \right)\]

1. The coefficient estimates will differ if a different baseline is used. But the fitted values, predictions, log odds between any pair of classes remain the same.

Multinomial Data

Rows: 200
Columns: 3
$ prog  <fct> vocation, general, vocation, vocation, vocation, general, vocati…
$ ses   <fct> low, middle, high, low, middle, high, middle, middle, middle, mi…
$ write <dbl> 35, 33, 39, 37, 31, 36, 36, 31, 41, 37, 44, 33, 31, 44, 35, 44, …

• Response:
  • prog (program type: general, academic, vocation)
• Predictors:
  • ses (social economic status: low, middle, high)
  • write (writing score)

Multinomial Logit - Variable Association

Program type is affected by social economic status

        prog
ses      general academic vocation
  low         16       19       12
  middle      20       44       31
  high         9       42        7

and writing score

          M  SD
general  51 9.4
academic 56 7.9
vocation 47 9.3

The level (coding order) of prog is

[1] "general"  "academic" "vocation"

Multinomial Logit - Setting Baseline

multino_data$prog2 <- relevel(multino_data$prog, ref = "academic")
levels(multino_data$prog2)

[1] "academic" "general"  "vocation"

• \(K = 3\) (academic = 1, general = 2, vocation = 3)
• For ses, low = 1, middle = 2, high = 3

\[\log \left( \frac{Pr(prog = general)}{Pr(prog = academic)}\right) = b_{10} + b_{11}(ses = 2) + b_{12}(ses = 3) + b_{13}write\]

\[\log \left( \frac{Pr(prog = vocation)}{Pr(prog = academic)}\right) = b_{20} + b_{21}(ses = 2) + b_{22}(ses = 3) + b_{23}write\]

• \(b_{13}\): All others held constant, the amount changed in the log odds of being in general vs. academic program as write increases one unit.

• \(b_{21}\) All others held constant, the amount changed in the log odds of being in vocation vs. academic program if moving from ses = "low" to ses = "middle".

set “academic” as the baseline category factor(multino_data$prog, levels = c(“general”, “vocation”, “academic”)

b13 A one-unit increase in the variable write is associated with the decrease in the log odds of being in general program vs. academic program in the amount of .058 . b23 A one-unit increase in the variable write is associated with the decrease in the log odds of being in vocation program vs. academic program. in the amount of .1136 . b12 The log odds of being in general program vs. in academic program will decrease by 1.163 if moving from ses=“low” to ses=“high”. b11 The log odds of being in general program vs. in academic program will decrease by 0.533 if moving from ses=“low”to ses=“middle”, although this coefficient is not significant. b22 The log odds of being in vocation program vs. in academic program will decrease by 0.983 if moving from ses=“low” to ses=“high”. b21 The log odds of being in vocation program vs. in academic program will increase by 0.291 if moving from ses=“low” to ses=“middle”, although this coefficient is not significant.

Multinomial Logit - nnet::multinom()

multino_fit <- nnet::multinom(prog2 ~ ses + write, data = multino_data, trace = FALSE)
summ <- summary(multino_fit)
summ$coefficients

         (Intercept) sesmiddle seshigh  write
general          2.9     -0.53   -1.16 -0.058
vocation         5.2      0.29   -0.98 -0.114

• glmnet() uses the softmax coding that treats all \(K\) classes symmetrically, and coefficients have a different meaning. (ISL eq. (4.13), (4.14))

• The fitted values, predictions, log odds between any pair of classes, and other key model outputs remain the same.

glmnet(x = input_matrix, y = categorical_vector, family = "multinom", 
       family = "multinomial", lambda = 0)

• Estimate coefficients for all \(K\) classes.
• The fitted values, predictions, log odds between any pair of classes, and other key model outputs remain the same.

Multinomial Logit - Estimated Probability

head(fitted(multino_fit))

  academic general vocation
1     0.15    0.34     0.51
2     0.12    0.18     0.70
3     0.42    0.24     0.34
4     0.17    0.35     0.48
5     0.10    0.17     0.73
6     0.35    0.24     0.41

• Hold write at its mean and examine the predicted probabilities for each level of ses.

dses <- data.frame(ses = c("low", "middle", "high"), 
                   write = mean(multino_data$write))
predict(multino_fit, newdata = dses, type = "probs")

  academic general vocation
1     0.44    0.36     0.20
2     0.48    0.23     0.29
3     0.70    0.18     0.12

https://stackoverflow.com/questions/22905807/how-does-the-function-multinom-from-r-package-nnet-compute-the-multinomial-proba

Multinomial Logit - Probability Curve

Generalized Linear Models

Generalized Linear Models in Greater Generality

• Conditional on \(\mathbf{X}\), the response \(Y\) belongs to a certain family of distribution.¹
  • Linear regression: Gaussian
  • Logistic regression: Bernoulli, binomial, multinomial

• Model the mean of \(Y\) as a function of the predictors.
  • Linear regression: \(E(Y \mid \mathbf{x}) = \mathbf{x}'\boldsymbol \beta\)
  • Logistic regression: \(E(Y \mid \mathbf{x}) = P(Y=1 \mid \mathbf{x}) = \pi(\mathbf{x}) = \frac{e^{\mathbf{x}'\boldsymbol \beta}}{1 + e^{\mathbf{x}'\boldsymbol \beta}}\)

• In general, with \(E(Y \mid \mathbf{x}) = \mu\), the link function \(\eta(\mu) = {\bf x}'\boldsymbol \beta\) transforms \(\mu\) so that the transformed mean is a linear function of predictors!
  • Linear regression: \(\eta(\mu) = \mu\)
  • Logistic regression: \(\eta(\mu) = \log(\mu/(1-\mu))\)

Any regression approach that follows this general recipe is known as a generalized linear model (GLM).

1. Usually the distribution of \(Y\) belongs to the exponential family.

Link Function

• Logistic regression uses the logit function \(\eta = g(\pi) = \ln\left( \dfrac{\pi}{1-\pi}\right)\) as the link function.

• \(\pi = \dfrac{1}{1 + e^{-\eta}} \in (0, 1)\) is the CDF of the logistic distribution, whose PDF is of the from \[f(\eta) = \frac{e^{-\eta}}{(1 + e^{-\eta})^2}, \quad \eta \in(-\infty, \infty)\]

• Could use a different link function and hence CDF to describe the probability (S-shaped) curve.

Probit and Complementary log-log (cloglog) Link

• If \(\pi = \Phi(\eta) \in (0, 1)\), \(\Phi(\cdot)\) is the CDF of standard normal distribution, the link function \[\eta = g(\pi) = \Phi^{-1}(\pi)\] is called probit, and the model is called probit model or probit regression.

• Another popular link function is the complementary log-log link: \[\eta = g(\pi) = \log\left( -\log(1-\pi)\right)\] where \(\pi = 1 - \exp(-\exp(\eta))\) is the CDF of the so called Gumbel distribution.¹

1. The complementary log-log link is actually defined by a negative Gumbel random variable. No worries about why it is used at this moment.

Link Function Summary

Distribution	Link Function \(\eta = g(\pi)\)	CDF \(\pi = g^{-1}(\eta)\)	PDF
Logistic	logit: \(\ln\left( \dfrac{\pi}{1-\pi}\right)\)	\(\dfrac{1}{1 + e^{-\eta}}\)	\(\dfrac{e^{-\eta}}{(1 + e^{-\eta})^2}\)
Normal	probit: \(\Phi^{-1}(\pi)\)	\(\Phi(\eta)\)	\(\frac{1}{\sqrt{2\pi}} e^{-\frac{\eta^2}{2}}\)
Gumbel	cloglog: \(\log\left( -\log(1-\pi)\right)\)	\(1 - \exp(-\exp(\eta))\)	\(e^{-(\eta + e ^ {-\eta})}\)

Any transformation that maps probabilities into the real line could be used to produce a GLM for binary classification, as long as the transformation is one-to-one continuous and differentiable.

\[\pi = F(\eta)\] \[\eta = F^{-1}(\pi)\]

Link Function Summary

Name	Link Function \(\eta = g(\pi)\)
logit	\(\ln\left( \dfrac{\pi}{1-\pi}\right)\)
probit	\(\Phi^{-1}(\pi)\)
cloglog	\(\log\left( -\log(1-\pi)\right)\)

• Logit and probit links produce similar curve. For simple regression, both estimate \(\pi = 1/2\) when \(x = -\beta_0/\beta_1\) and exhibit symmetric behavior.
• The complementary log-log link is not symmetric.

PDF

• Normal and logistic density are symmetric, while Gumbel is right skewed.

Probability Curve

Probit and Complementary log-log Links

probit_fit <- glm(default ~ balance, data = Default, family = binomial(link = "probit"))
cloglog_fit <- glm(default ~ balance, data = Default, family = binomial(link = "cloglog"))

Other Topics

• Repeated measures and binomial logistic regression

• Regression diagnostics for binary data

• Penalized logistic regression

• Exponential family

• Poisson regression

https://grodri.github.io/glms/

https://stats.oarc.ucla.edu/r/dae/multinomial-logistic-regression/

https://glmnet.stanford.edu/articles/glmnet.html