Tree-based Methods

MSSC 6250 Statistical Machine Learning

Dr. Cheng-Han Yu
Department of Mathematical and Statistical Sciences
Marquette University

Tree-based Methods

• Can be used for regression and classification.

• IDEA: Segmenting the predictor space into many simple regions.

• Simple, useful for interpretation, and has nice graphical representation.

• Not competitive with the best supervised learning approaches in terms of prediction accuracy. (Large bias)

• Combining a large number of trees (ensembles) often results in improvements in prediction accuracy, at the expense of some loss interpretation.

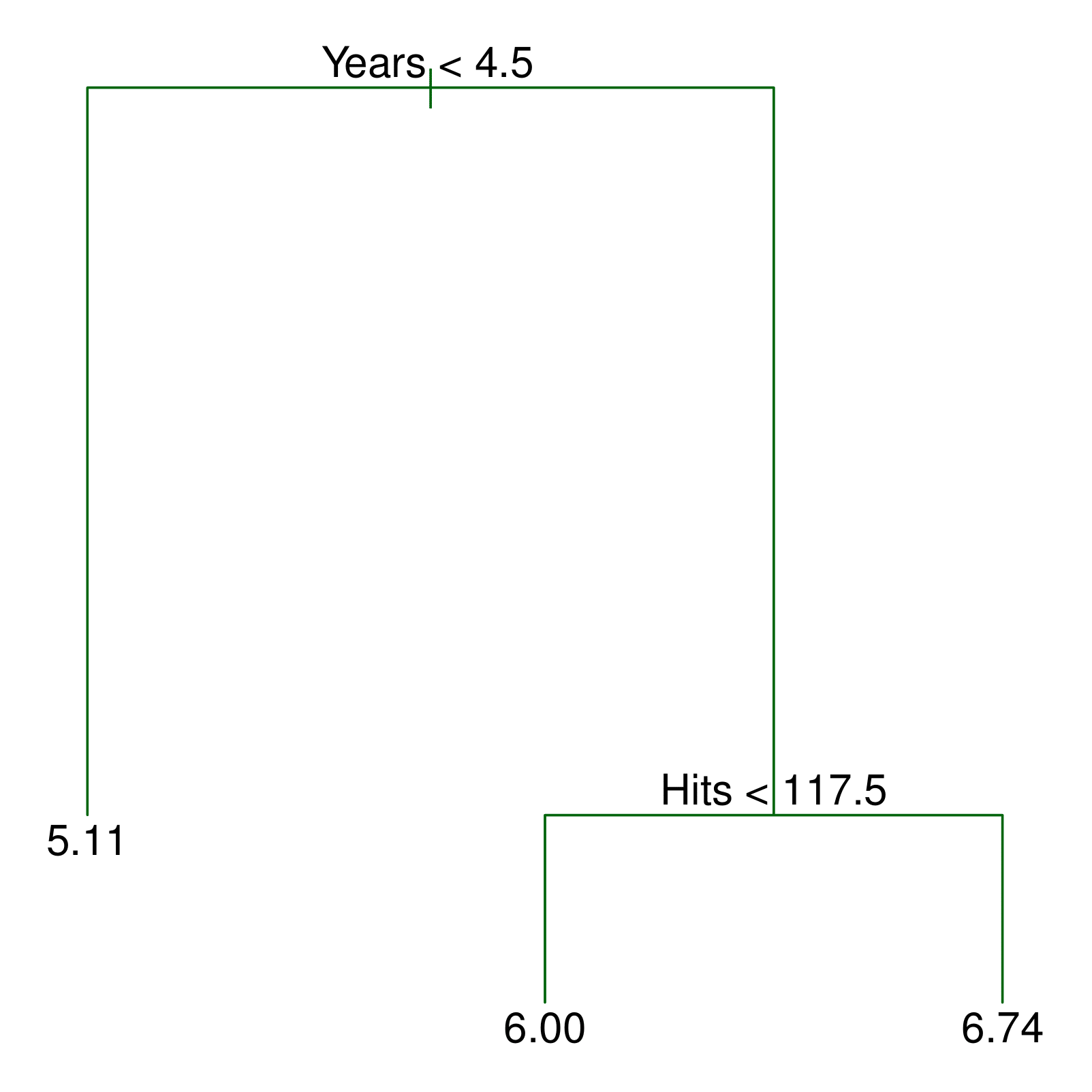
Decision Trees: Classification and Regression Trees (CART)

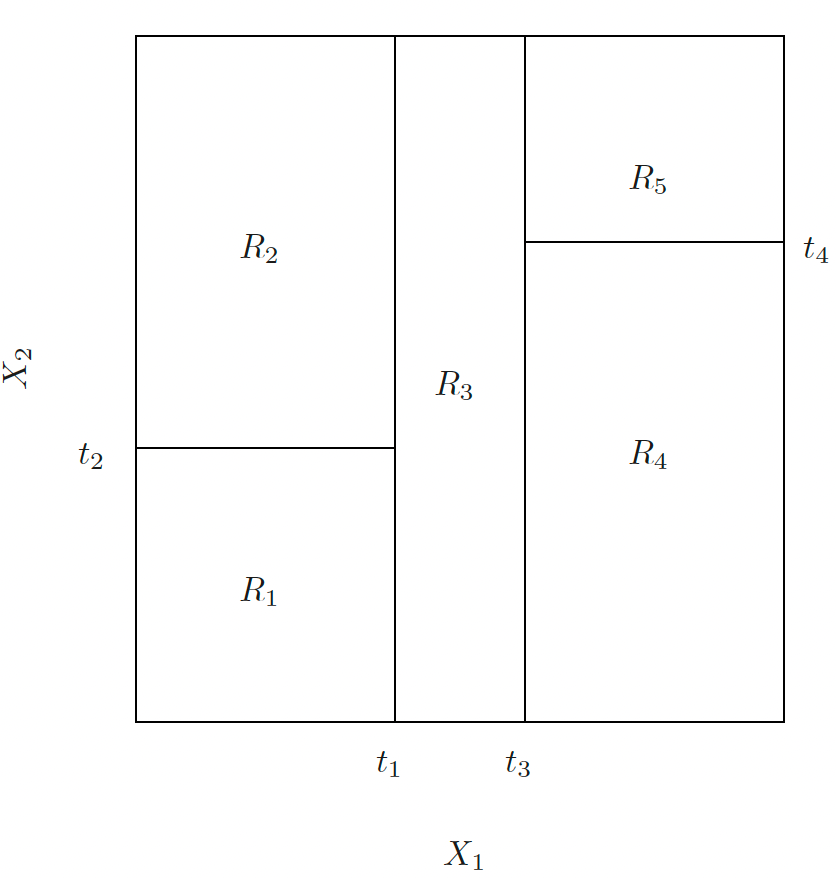
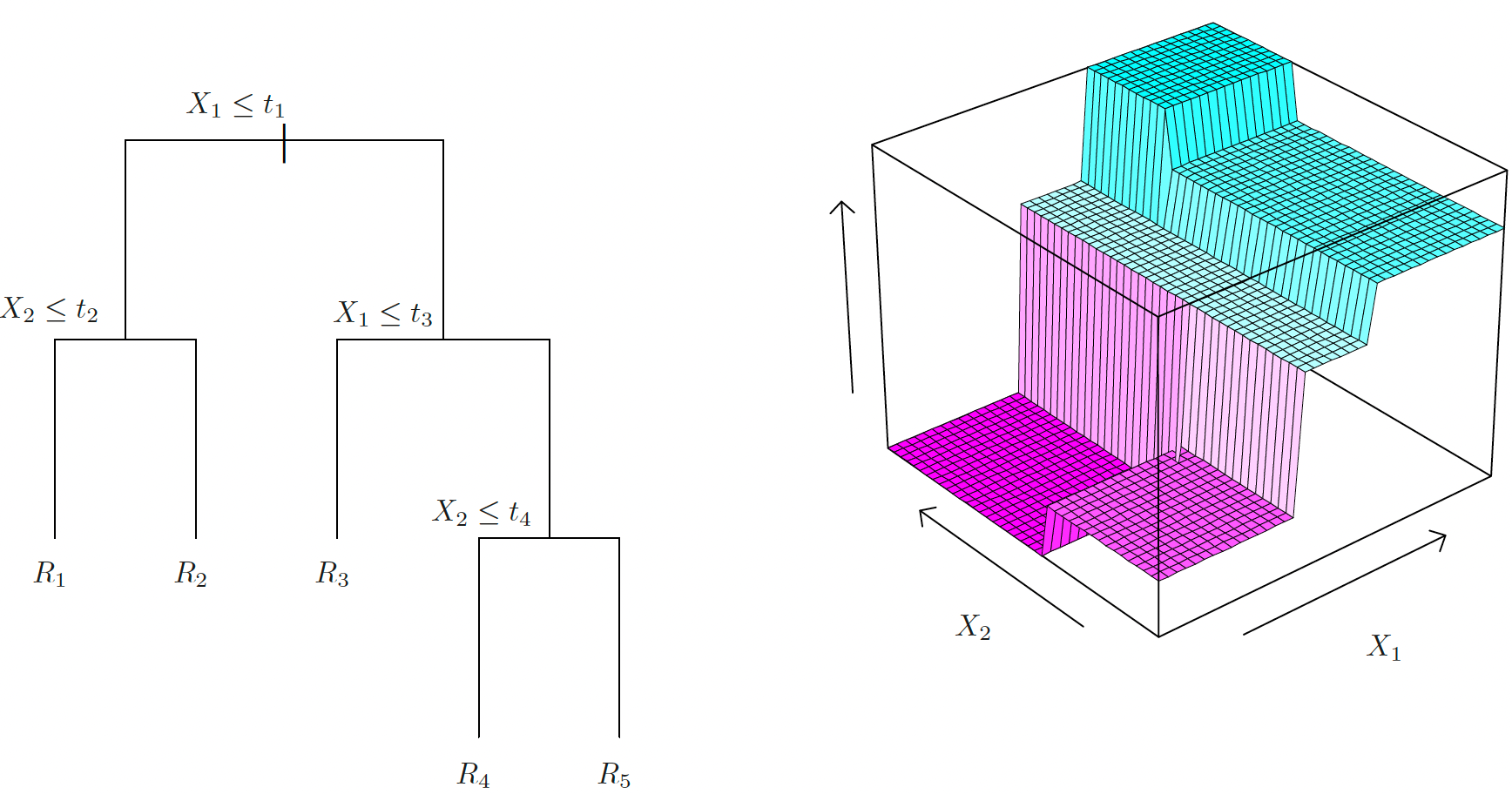
• CART is a nonparametric method that recursively partitions the feature space into hyper-rectangular subsets (boxes), and make prediction on each subset.

• Divide the predictor space — the set of possible values for \(X_1, X_2, \dots, X_p\) — into \(J\) distinct and non-overlapping regions, \(R_1, R_2, \dots, R_J\).

• For every test point that falls into the region \(R_j\) , we make the same prediction:
  • Regression: the mean of the response values for the training points in \(R_j\).
  • Classification: the most commonly occurring class of training points in \(R_j\).

Recursive Binary Splitting

• Computationally infeasible to consider every possible partition of the feature space into \(J\) boxes.

• The recursive binary splitting is top-down and greedy:
  • Top-down: begins at the top of the tree
  • Greedy: at each step, the best split is made at that particular step, rather than looking ahead and picking a split that will lead to a better tree in some future step.

• Select \(X_j\) and a cutoff \(s\) so that splitting the predictor space into \(\{\mathbf{X}\mid X_j < s \}\) and \(\{\mathbf{X}\mid X_j \ge s \}\) leads to the greatest possible reduction in
  • \(SS_{res}\) for regression
  • Gini index, entropy or misclassification rate for classification
• Repeatedly split one of the two previously identified regions until a stopping criterion is reached.

at each step of the tree-building process

Classification Tree

• KNN requires K and a distance measure.

• SVM requires kernels.

• Tree solves this by recursively partitioning the feature space using a binary splitting rule \(\mathbf{1}\{x \le c \}\)

• 0: Red; 1: Blue

Classification Tree

If \(x_2 < -0.64\), \(y = 0\).

Classification Tree

If \(x_2 \ge -0.64\) and \(x_1 \ge 0.69\), \(y = 0\).

Classification Tree

If \(x_2 \ge -0.64\), \(x_1 < 0.69\), and \(x_2 \ge 0.75\), \(y = 0\).

Classification Tree

If \(x_2 \ge -0.64\), \(x_1 < 0.69\), \(x_2 < 0.75\), and \(x_1 < -0.69\), \(y = 0\).

Classification Tree

Step 5 may not be beneficial.

Classification Tree

Step 6 may not be beneficial. (Could overfit)

Classification Tree

Step 7 may not be beneficial. (Could overfit)

Misclassification Rate

• The classification error rate is the fraction of the training observations in that region that do not belong to the most common class: \[1 - \max_{k} (\hat{p}_{mk})\] where \(\hat{p}_{mk}\) is the proportion of training observations in the \(m\)th region that are from the \(k\)th class.

• Classification error is not sensitive for tree-growing.

• Ideally hope to have nodes (regions) including training points that belong to only one class.

Gini Index (Impurity)

The Gini index is defined by

\[\sum_{k=1}^K \hat{p}_{mk}(1 - \hat{p}_{mk})\] which is a measure of total variance across the K classes.

• Gini is small if all of the \(\hat{p}_{mk}\)s are close to zero or one.

• Node purity: a small value indicates that a node contains predominantly observations from a single class.

Shannon Entropy

The Shannon entropy is defined as

\[- \sum_{k=1}^K \hat{p}_{mk} \log(\hat{p}_{mk}).\] - The entropy is near zero if the \(\hat{p}_{mk}\)s are all near zero or one.

• Gini index and the entropy are similar numerically.

Any of these three approaches might be used when pruning the tree, but the classification error rate is preferable if prediction accuracy of the final pruned tree is the goal.

Comparing Measures

• Misclassification can be used for evaluating a tree, but may not be sensitive enough for building a tree.

For each quantity, smaller value means that the node is more “pure”, hence, there is a higher certainty when we predict a new value. The idea of splitting a node is that, we want the two resulting child node to contain less variation. In other words, we want each child node to be as “pure” as possible.

Regression Tree

The goal is to find boxes \(R_1, \dots ,R_J\) that minimize the \(SS_{res}\), given by \[\sum_{j=1}^J\sum_{i \in R_j}\left( y_i - \hat{y}_{R_j}\right)^2\] where \(\hat{y}_{R_j}\) is the mean response for the training observations within \(R_j\).

Source: ISL Fig 8.3

Tree Pruning

• Using regression and classification performance measures to grow trees with no penalty on the tree size leads to overfitting.

• Cost complexity pruning:

Given the largest tree \(T_{max}\),

\[\begin{align} \min_{T \subset T_{max}} \sum_{m=1}^{|T|}\sum_{i:x_i\in R_m} \left( y_i - \hat{y}_{R_m}\right)^2 + \alpha|T| \end{align}\] where \(|T|\) indicates the number of terminal nodes of the tree \(T\).

• Large \(\alpha\) results in small trees

• Choose \(\alpha\) using CV

• Algorithm 8.1 in ISL for building a regression tree.

• Replace \(SS_{res}\) with misclassification rate for classification.

Implementation

• rpart::rpart()

library(rpart)
rpart::rpart(formula = y ~ x1 + x2, data)

• tree::tree()

library(tree)
tree::tree(formula = y ~ x1 + x2, data)

• sklearn tree

from sklearn import tree
dtc = tree.DecisionTreeClassifier()
dtc = dtc.fit(X, y)
dtr = tree.DecisionTreeRegressor()
dtr = dtr.fit(X, y)

Trees v.s. Linear Regression

Linear regression

\[f(X) = \beta_0 + \sum_{j=1}^pX_j\beta_j\]

• Performs better when the relationship between \(y\) and \(x\) is approximately linear.

Regression tree

\[f(X) = \sum_{j=1}^J \hat{y}_{R_j}\mathbf{1}(\mathbf{X}\in R_j)\]

• Performs better when there is a highly nonlinear and complex relationship between \(y\) and \(x\).

• Preferred for interpretability and visualization.

Trees v.s. Linear Models

Source: ISL Fig 8.7

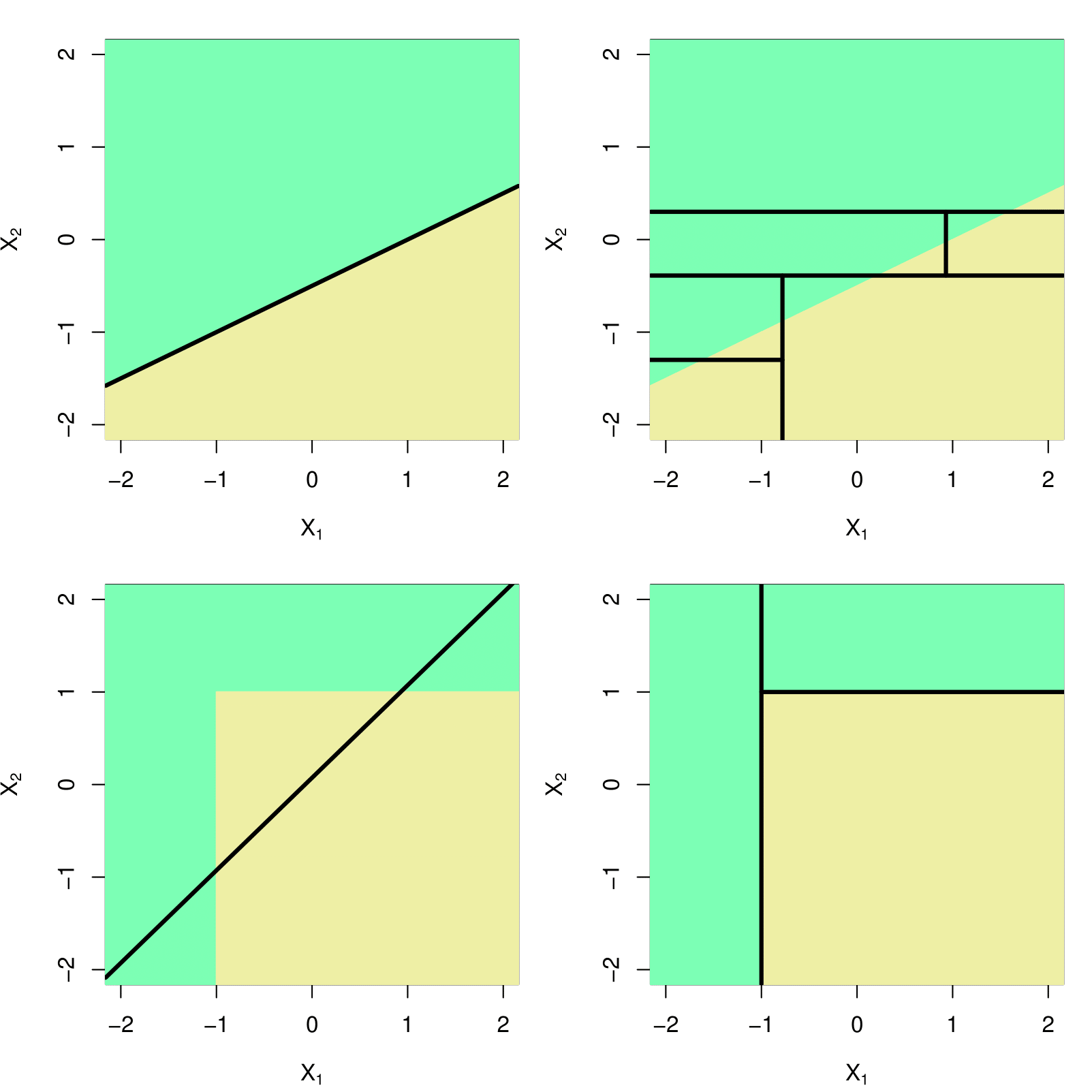
Ensemble Learning: Bagging, Random Forests, Boosting

Two heads are better than one, not because either is infallible, but because they are unlikely to go wrong in the same direction. – C.S. Lewis, British Writer (1898 - 1963)

『三個臭皮匠，勝過一個諸葛亮』

Ensemble Methods

• An ensemble method combines many weak learners (unstable, less accurate) to obtain a single and powerful model.

• The CARTs suffer from high variance.

• If independent \(Z_1, \dots, Z_n\) have variance \(\sigma^2\), then \(\bar{Z}\) has variance \(\sigma^2/n\).

• Averaging a set of observations reduces variance!

With \(B\) separate training sets,

\[\hat{f}_{avg}(x) = \frac{1}{B}\sum_{b=1}^B\hat{f}_{b}(x)\]

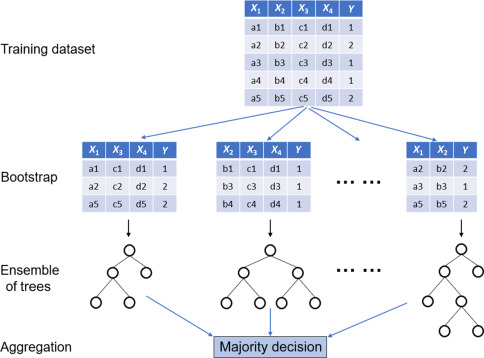
Bagging

• Bootstrap aggregation, or bagging is a procedure for reducing variance.

• Generate \(B\) bootstrap samples by repeatedly sampling with replacement from the training set \(B\) times.

\[\hat{f}_{bag}(x) = \frac{1}{B}\sum_{b=1}^B\hat{f}^*_{b}(x)\]

Source: Wiki page of bootstrap aggregating

Bagging works for many regression methods, but it is particularly useful for decision trees.

Bagging on Decision Trees

Source: Wiki page of ensemble learning

CART v.s. Bagging

• For CART, the decision line has to be aligned to axis.

• For Bagging, \(B = 200\) each having 400 training points. Boundaries are smoother.

Notes of Bagging

• Using a very large \(B\) will not lead to overfitting.

• Use \(B\) sufficiently large that the error has settled down.

• Bagging improves prediction accuracy at the expense of interpretability.

• When different trees are highly correlated, simply averaging is not very effective.

• If there is one very strong predictor in the data set, in the collection of bagged trees, most or all of the trees will use this strong predictor in the top split. Therefore, all of the bagged trees will look quite similar to each other.

• The predictions from the bagged trees will be highly correlated, and hence averaging does not lead to as large reduction in variance.

• Use many trees and averaging. It is no longer clear which variables are most important to the procedure.

• If there is one very strong predictor in the data set, in the collection of bagged trees, most or all of the trees will use this strong predictor in the top split. Therefore, all of the bagged trees will look quite similar to each other.

• The predictions from the bagged trees will be highly correlated, and hence averaging does not lead to as large reduction in variance.

Random Forests

• Random forests improve bagged trees by decorrelating the trees.

• \(m\) predictors are randomly sampled as split candidates from the \(p\) predictors.

Source: Misra and Li in Machine Learning for Subsurface Characterization (2020)

• When building decision trees, each time a split in a tree is considered, a random sample of \(m\) predictors is chosen as split candidates from the full set of \(p\) predictors.

• The split is allowed to use only one of those \(m\) predictors.

Random Forests

• \(m \approx \sqrt{p}\) for classification; \(m \approx p/3\) for regression.

• Decorrelating: on average \((p − m)/p\) of the splits will not even consider the strong predictor, and so other predictors will have more of a chance.

• If \(m = p\), random forests = bagging.

• The improvement is significant when \(p\) is large.

CART vs. Bagging vs. Random Forests

• randomForest::randomForest(x, y, mtry, ntree, nodesize, sampsize)

Boosting

• Bagging trees are built on bootstrap data sets, independent with each other.

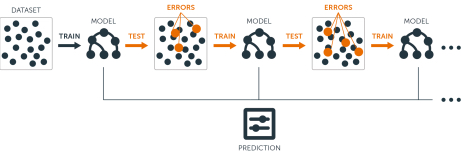
• Boosting¹ trees are grown sequentially: each tree is grown using information from previously grown trees.

• Boosting does not involve bootstrap sampling; instead each tree is fit on a modified version of the original data set, the residuals!

Source: Fig. 12.1 of Hands-on Machine Learning with R

1. Boosting can also be applied to many models, but most effectively applied to decision trees.

Boosting

• Base (weak) learners: Could any simple model (high-bias low-variance). Usually a decision tree.

• Training weak models: Fit a (shallow) tree \(\hat{f}^b\) with relatively few \(d\) splits

• Sequential Training w.r.t. residuals: Fitting each tree in the sequence to the previous tree’s residuals.

Suppose our final tree is \(\hat{f}(x)\) that starts with \(0\).

1. Fit a decision tree \(\hat{f}^1\) to \(\{ y_i \}\)
2. Grow the tree: \(\hat{f}(x) = \lambda\hat{f}^1\)
3. Fit the next decision tree \(\hat{f}^2\) to the residuals of the previous fit \(\{ e^1_i\} = \{ y_i - \lambda\hat{f}^1(x_i)\}\)
4. Grow the tree: \(\hat{f}(x) = \lambda\hat{f}^1 + \lambda\hat{f}^2\)
5. Fit the next decision tree \(\hat{f}^3\) to the residuals of the previous fit \(\{ e^2_i \} = \{ e^1_i - \lambda\hat{f}^2(x_i)\}\)
6. Grow the tree: \(\hat{f}(x) = \lambda\hat{f}^1 + \lambda\hat{f}^2 + \lambda\hat{f}^3\)

Boosting

• The final boosting tree is \[\hat{f}(x) = \sum_{b=1}^B\lambda\hat{f}^b(x)\]
• Tuning parameters
  • Number of base trees \(B\): Large \(B\) can overfit. Use cross-validation to choose \(B\).
  • Number of base tree splits \(d\): Often \(d=1\) works well. The growth of a tree takes into account the other grown trees, so small trees are sufficient.
  • Shrinkage \(\lambda > 0\): Controls the learning rate of boosting. Usual values are 0.01 or 0.001. Small \(\lambda\) needs large \(B\).

Boosting for Classification

• distribution = "bernoulli": LogitBoost

gbm.fit = gbm(y ~ ., data = data.frame(x1, x2, y), 
              distribution = "bernoulli", 
              n.trees = 10000, shrinkage = 0.01, bag.fraction = 0.6, 
              interaction.depth = 2, cv.folds = 10)

Boosting Cross Validation

gbm.perf(gbm.fit, method = "cv")

[1] 1181

Boosting for Regression

gbm.fit <- gbm::gbm(y ~ x, data = data.frame(x, y), 
                    distribution = "gaussian", n.trees = 300,
                    shrinkage = 0.5, bag.fraction = 0.8,
                    cv.folds = 10)

Boosting for Regression

Other Topics

• AdaBoost (Adaptive Boosting) gbm(y ~ ., distribution = "adaboost")

• Gradient Boosting/Extreme Gradient Boosting (XGBoost) xgboost

  • http://uc-r.github.io/gbm_regression
  • https://xgboost.readthedocs.io/en/stable/R-package/xgboostPresentation.html
  • https://github.com/dmlc/xgboost
  • https://cran.r-project.org/web/packages/xgboost/xgboost.pdf

• Bayesian Additive Regression Trees (BART) (ISL Sec. 8.2.4)

https://jamleecute.web.app/gradient-boosting-machines-gbm/